Modulus & Argument (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Argand diagrams - basics
What is an Argand diagram?
An Argand diagram is a geometrical way to represent complex numbers as either a point or a vector in two-dimensional space
We can represent the complex number
by the point with cartesian coordinate
The real component is represented by points on the x-axis, called the real axis, Re
The imaginary component is represented by points on the y-axis, called the imaginary axis, Im


You may be asked to show roots of an equation in an Argand diagram
First solve the equation
Draw a quick sketch, only adding essential information to the axes
Plot the points and label clearly
How can I use an Argand diagram to visualise |z1 + z2| and |z1 - z2|?
Plot two complex numbers z1 and z2
Draw a line from the origin to each complex number
Form a parallelogram using the two lines as two adjacent sides
The modulus of their sum |z1 + z2| will be the length of the diagonal of the parallelogram starting at the origin
The modulus of their difference |z1 - z2| will be the length of the diagonal between the two complex numbers

Worked Example
a) Plot the complex numbers z1 = 2 + 2i and z2 = 3 – 4i as points on an Argand diagram.

b) Write down the complex numbers represented by the points A and B on the Argand diagram below.

Examiner Tips and Tricks
When setting up an Argand diagram you do not need to draw a fully scaled axes, you only need the essential information for the points you want to show, this will save a lot of time.
Modulus & argument
How do I find the modulus of a complex number?
The modulus of a complex number is its distance from the origin when plotted on an Argand diagram
The modulus of
is written
If
, then we can use Pythagoras to show…
A modulus is always positive
the modulus is related to the complex conjugate by…
This is because
In general,
e.g. both
and
have a modulus of 5, but
simplifies to
which has a modulus of 8

How do I find the argument of a complex number?
The argument of a complex number is the anti-clockwise angle that it makes when starting at the positive real axis on an Argand diagram
Arguments are measured in radians
Sometimes these can be given exact in terms of
The argument of
is written
Arguments can be calculated using right-angled trigonometry
This involves using the tan ratio plus a sketch to decide whether it is positive/negative and acute/obtuse
Arguments are usually given in the range
This is called the principal argument
Negative arguments are for complex numbers in the third and fourth quadrants
Occasionally you could be asked to give arguments in the range
The argument of zero,
is undefined (no angle can be drawn)

Examiner Tips and Tricks
Always draw a sketch to see which quadrant the complex number is in
Worked Example
a) Find the modulus and argument of
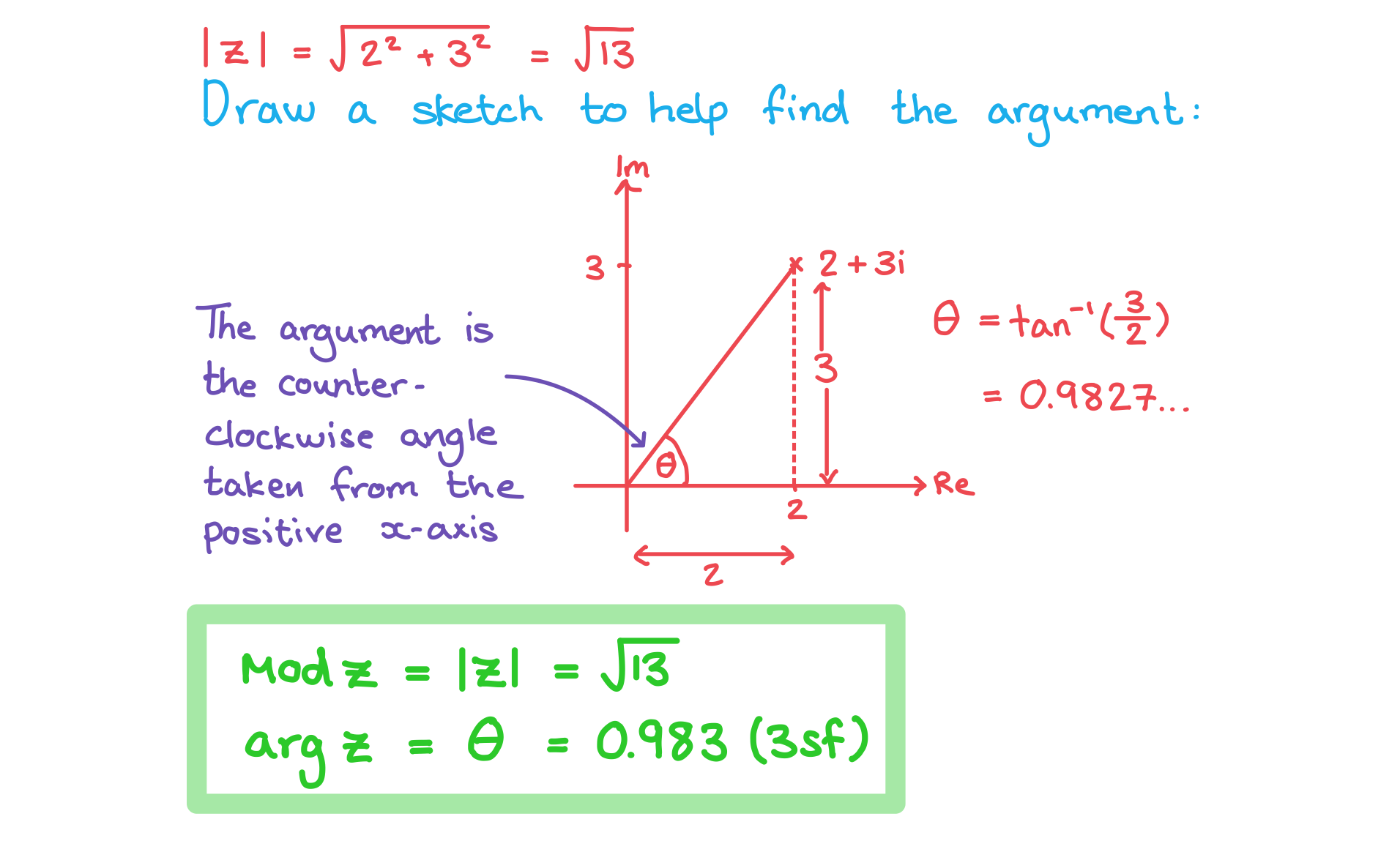
b) Find the modulus and argument of


Unlock more, it's free!
Did this page help you?