The Negative Binomial Distribution (Edexcel A Level Further Maths) : Revision Note
Conditions for Negative Binomial Models
What is the negative binomial distribution?
The negative binomial distribution models the number of trials needed to reach a fixed number of successes,
For example, how many times will you have to roll a dice until it lands on a '6' for the third time
There is no one standard form of notation for the negative binomial distribution
But for a random variable
that has the negative binomial distribution you could write either:
or
is the number of trials that will be required to reach a total of
successes
is the fixed probability of success in any one trial
What are the conditions for using a negative binomial model?
A negative binomial model can be used for an experiment that satisfies the following conditions:
The experiment consists of an indefinite number of successive trials
The outcome of each trial is independent of the outcomes of all other trials
There are exactly two possible outcomes for each trial (success and failure)
The probability of success in any one trial (
) is constant
Note that these conditions are very similar to the conditions for the binomial distribution
But for a binomial distribution the number of trials (
) is fixed
And you count the number of successes
While for a negative binomial distribution the number of successes (
) is fixed
And you count the number of trials it takes to reach that number of successes
When might the conditions not be satisfied?
If asked to criticise a negative binomial model, you may be able to question whether the trials are really independent
For example, someone may be repeating an activity until they achieve the
th success
The trials may not be independent because the person gets better from practising the activity
This also means the probability of success,
, is not constant
In order to proceed using the model, you will have to assume trials are independent
Examiner Tips and Tricks
Replace the word "trials" with the context (e.g. "flips of a coin") when commenting on conditions and assumptions
Negative Binomial Probabilities
What are the probabilities for the negative binomial distribution?
If
, then
has the probability function:
the random variable
is the number of trials needed to get
successes
is the constant probability of success in one trial
is the probability that the
success will occur on the
trial
Note that that is the product of
the binomial probability of getting
successes in
trials,
,
and the probability of getting a success in the
trial,
is the binomial coefficient
i.e.,
Also note that there is no greatest possible value of
It could require any number of trials to reach the
success
However for any given
,
gets closer and closer to zero as
gets larger
Where does the formula come from?
Consider rolling a fair dice and wanting to know the probability that it would take 12 rolls for the dice to land on '6' a total of 3 times
This is the same as saying that the third '6' occurs on the 12th roll
You can model this situation using the random variable
'success' here is defined as 'roll a 6'
because we're interested in the number of trials required to reach a total of 3 successes
is the probability of rolling a '6' on a fair dice
is the number of trials that will be required to reach 3 successes
The probability you are looking for is therefore
For the third '6' to occur on the 12th roll, the following things need to happen:
'6' must occur exactly 2 times in the first 11 rolls
It doesn't matter which rolls those two '6's occur on
The probability of that happening is
, for
So that part of the answer is a binomial probability
Then a '6' must also occur on the 12th roll
The probability of that happening is
So the probability of both those things happening is
That same logic can be used to find the general formula for negative binomial probabilities
Is there a connection between negative binomial probabilities and geometric probabilities?
Note that when
,the negative binomial probability function becomes:
That is the same as the geometric distribution probability function
The geometric distribution is the 'special case' of the negative binomial distribution when
Examiner Tips and Tricks
Make sure you are clear about what
,
,
and
refer to in the formula!
Read the question carefully to determine whether binomial, geometric or negative binomial probabilities are required
Worked Example
Emanuel is playing in a chess tournament, where his probability of winning any one game is 0.55. Find the probability that:
a) his first win is in the third game he plays
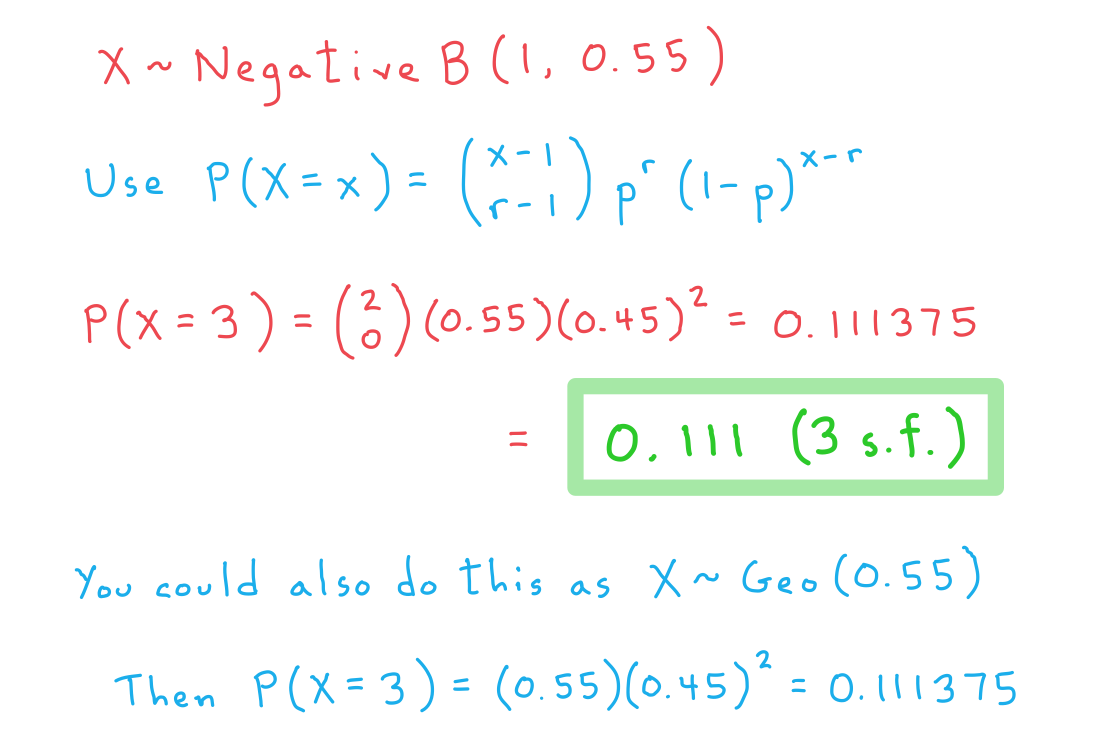
b) he wins exactly 4 of his first 7 games

c) he wins for the fourth time in his seventh game

d) he wins for the fourth time in his seventh game, given that he won his first game

e) his fourth win occurs in or before his seventh game.

f) Criticise the model used in this question.

Negative Binomial Mean & Variance
What are the mean and variance of the negative binomial distribution?
If
, then
The mean of
is
The variance of
is
You need to be able to use these formulae to answer questions about the negative binomial distribution.
Examiner Tips and Tricks
If a question gives you the mean and/or variance with one known parameters (
or
), form an equation to find the other
Worked Example
Croesus is tossing a biased coin for which the probability of the coin landing on 'heads' is . The random variable
represents the number of times he needs to flip the coin until it has landed on heads four times. Given that the mean of
is 10, find:
a) the value of
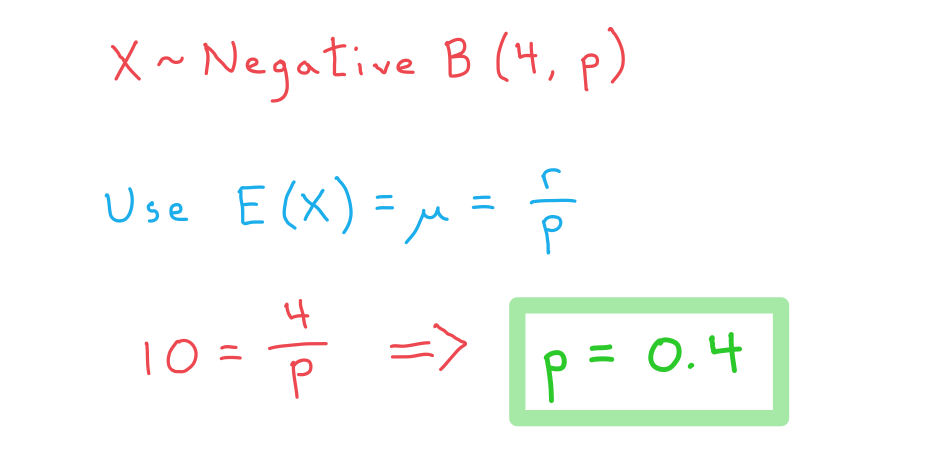
b) the standard deviation of
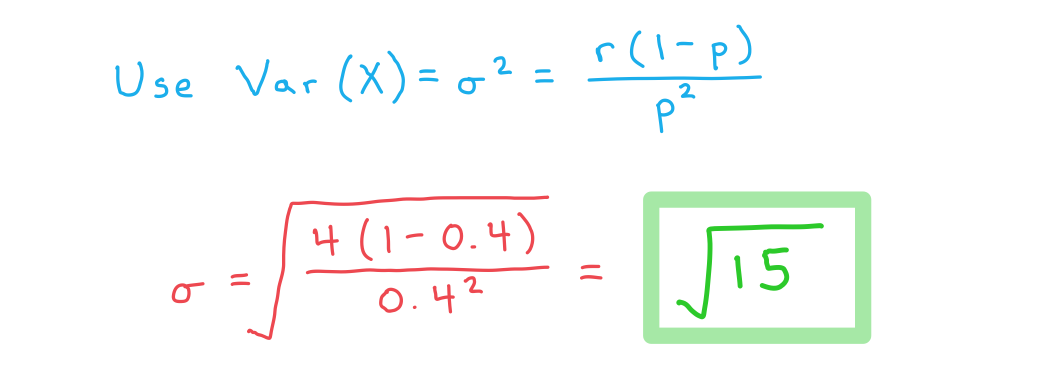
c) the probability that the fourth 'head' will occur on the seventh toss.
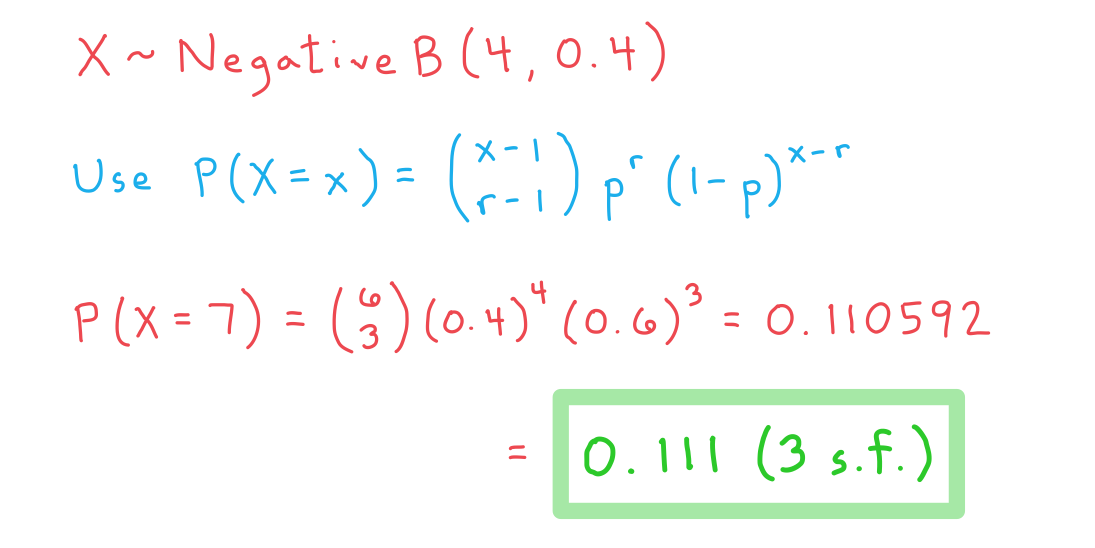

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
