Oblique Collisions of Two Spheres (Edexcel A Level Further Maths) : Revision Note
Oblique Collisions of Two Spheres
What is an oblique collision between two spheres?
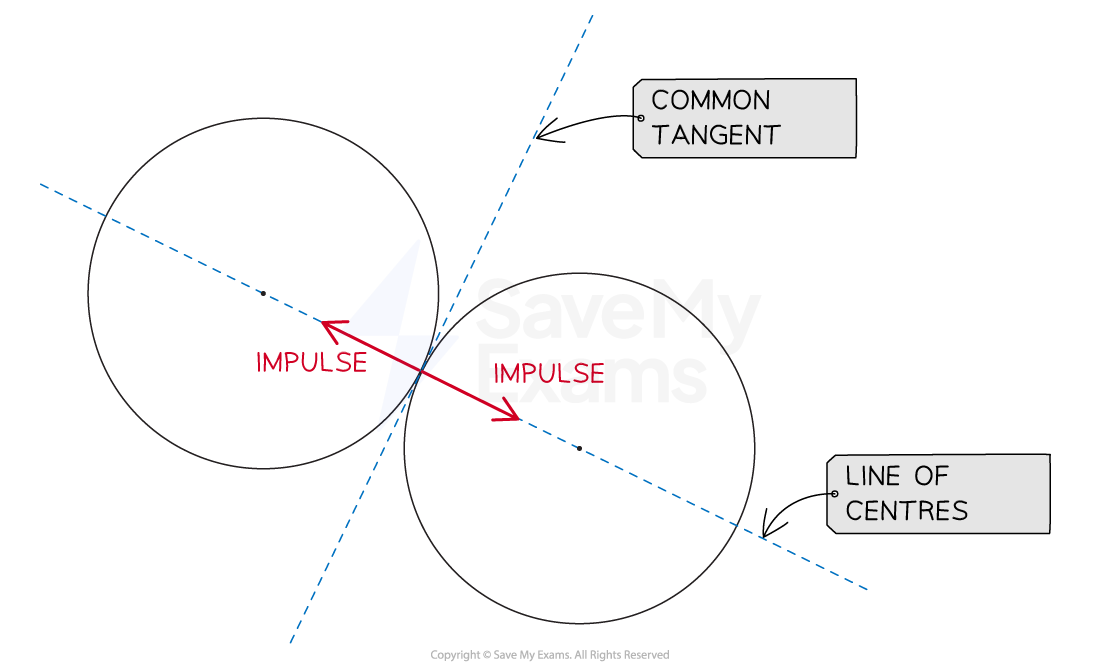
An oblique collision between two spheres is when two spheres which are not travelling along the same straight line collide
For the purposes of this course, the spheres are modelled as smooth, and as having equal radii
When they collide, they touch at a single point, and so share a common tangent
Perpendicular to the common tangent, is the line of centres, which passes through the centre of both spheres
Similar to when colliding with a surface, the objects only meet at a single point,
so the impulse only acts perpendicular to the 'surface',
in this case the 'surface' is another sphere
Therefore the impulse acts along the line of centres
How do I solve problems involving oblique collisions between two spheres?
The diagram below shows how to model the collision of spheres A and B, moving with speeds and
at angles
and
respectively to the line of centres. (Note that the line of centres has been drawn horizontally in this diagram, but all the expressions shown will be exactly the same whatever the direction of the line of centres is.)
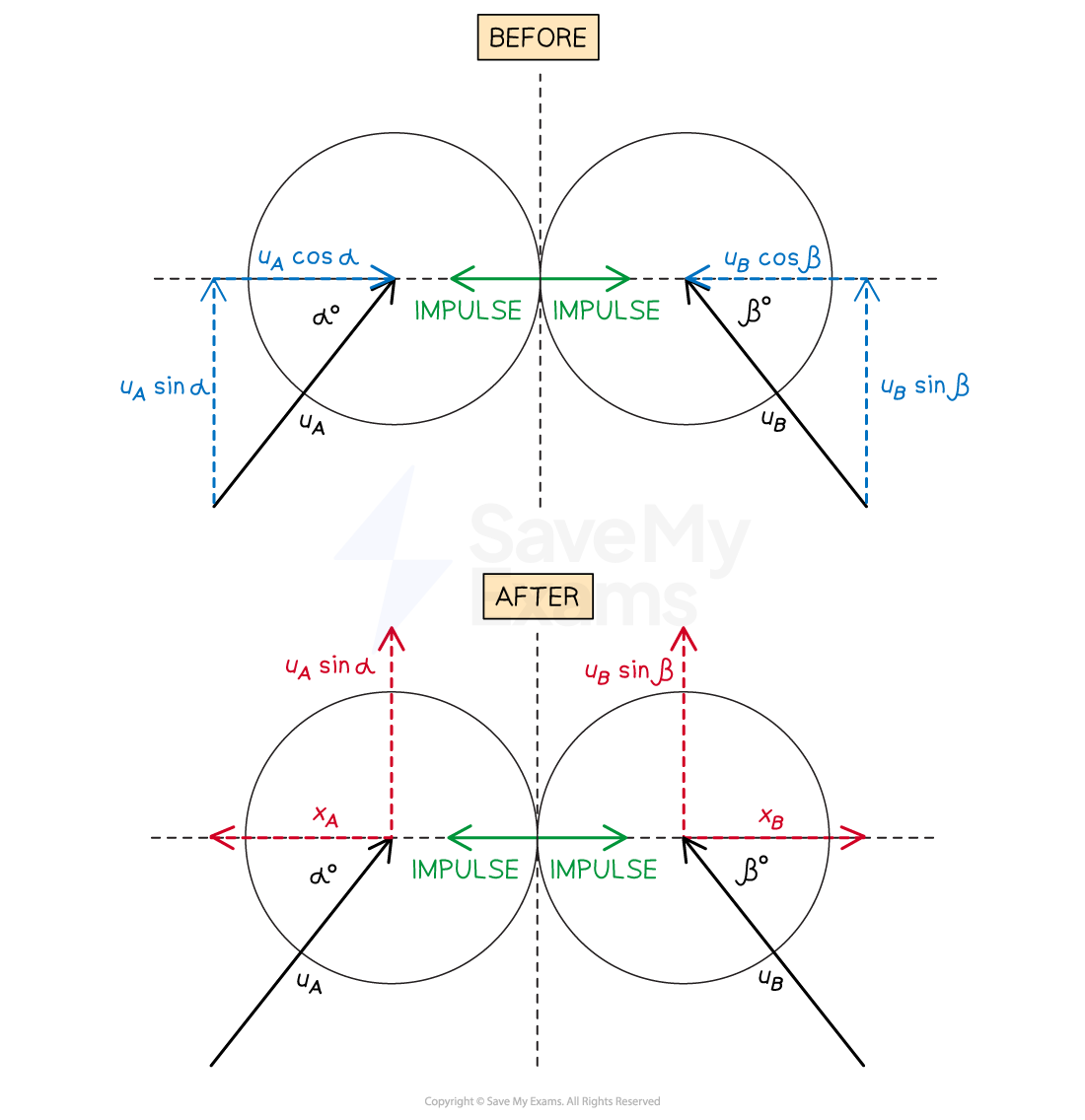
As the impulse only acts along the line of centres, it is only this component of the velocity which will be affected
In the diagram it can be seen that for the components parallel to the line of centres:
becomes
; the 'line of centres' component of A after the collision
becomes
; the 'line of centres' component of B after the collision
and
can be calculated later
The component of the velocity perpendicular to this, which is in the direction of the common tangent, is unaffected by the collision
In the diagram it can be seen that for the components parallel to the common tangent:
is still the 'common tangent' component of A after the collision
is still the 'common tangent' component of B after the collision
To find the components which have been affected by the impulse,
and
, we can:
Apply conservation of linear momentum in the direction of the impulse
Conservation of linear momentum:
Applied to the diagram above in the direction of the impulse, assuming A and B have masses
and
respectively:
Apply Newton's law of restitution
Newton's law of restitution:
Applied to the diagram above, in the direction of the impulse:
This will lead to a pair or simultaneous equations which can be solved to find
and
Be careful with positive and negative signs when forming these equations, the signs of the velocities will depend on how they are modelled in the diagram
e.g. If the arrows are drawn pointing away from each other in the "after" diagram, the speed of separation will be
If the arrows were drawn both pointing to the right, the speed of separation would be
Once all the components of the velocities of the spheres after the collision are known,
the speeds can be calculated using Pythagoras
the angle each sphere travels at can be calculated using right-angled trigonometry
Examiner Tips and Tricks
Drawing a bigger diagram will enable you to have more room for all the information and workings
This can help reduce errors caused by squashed writing!
You can choose whether to draw separate "before" and "after" diagrams, or combine them into one
Try both to see which you prefer
Worked Example
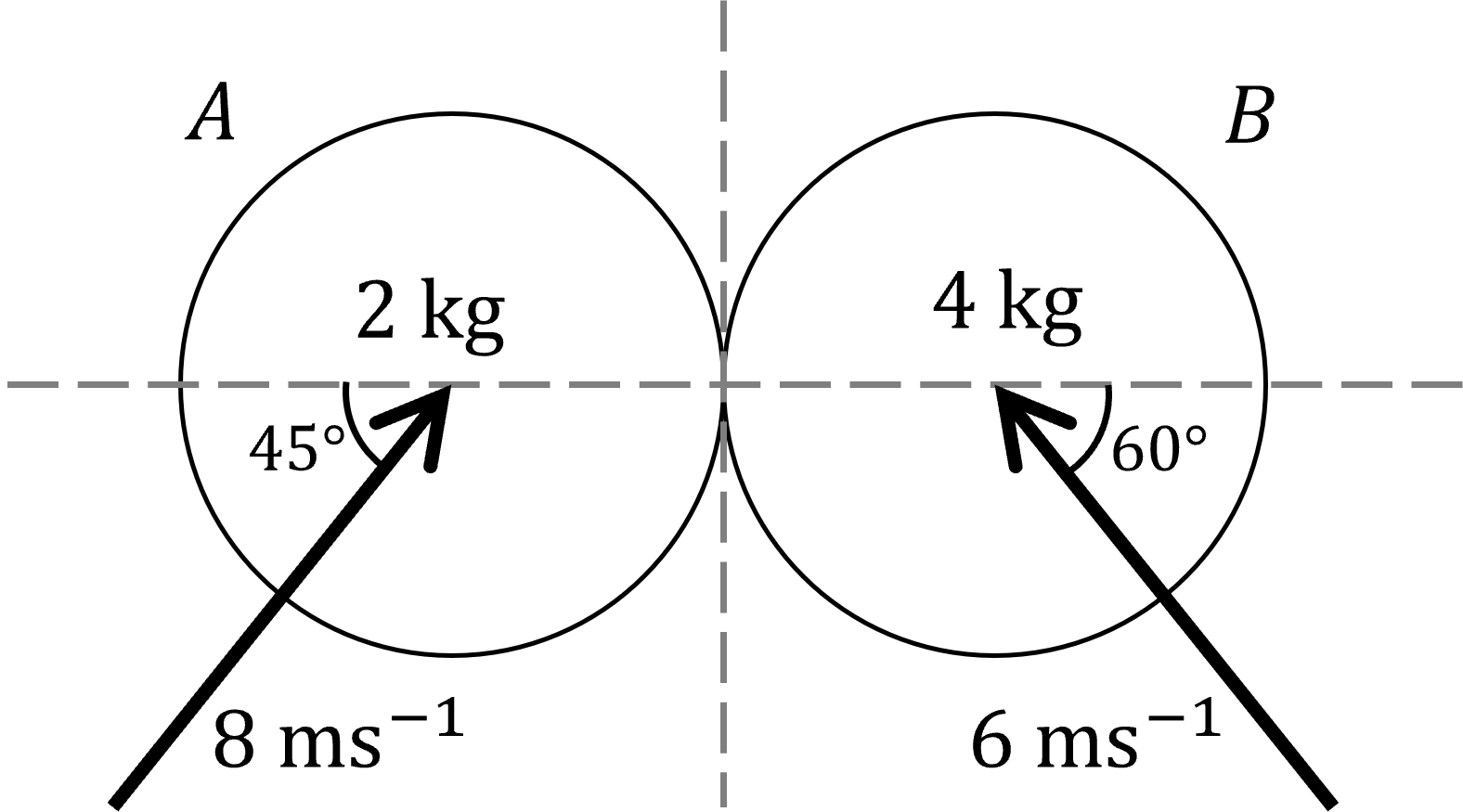
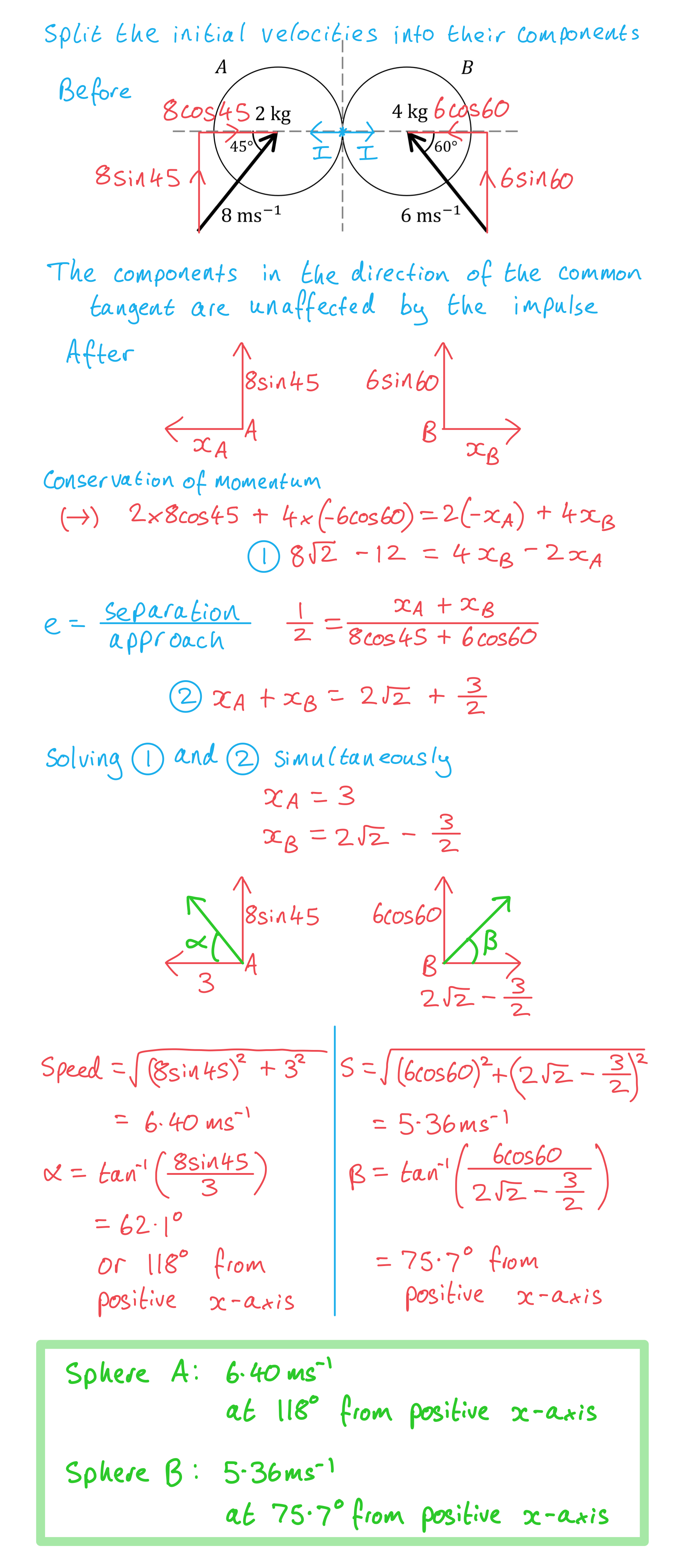
A small smooth sphere A of mass 2 kg collides with a small smooth sphere B of mass 4 kg. Immediately before the impact A is moving with a speed of 8 ms-1 in a direction 45° to the line of centres, and B is moving with speed 6 ms-1 in a direction 60° to the line of centres, as shown in the diagram. The coefficient of restitution between the two spheres is .
Find the speed and direction of each sphere after the collision.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?