Successive Collisions in 1D (Edexcel A Level Further Maths) : Revision Note
Successive Collisions in 1D
Can there be successive/multiple collisions?
After two objects collide it is possible that one (or both) of them collides with something else such as
A third object
A wall (perpendicular to the motion)
Deal with each collision separately and use the steps for direct collisions
Drawing a separate diagram for each collision can help
Be clear and unambiguous with labelling and variables
e.g.
is usually the speed after the first collision, so
may be used for the speed after the second collision
Can there be a second collision between the original two objects?
Let A, B and C be three objects travelling in the same straight line and suppose A and B collide directly and subsequently B and C collide directly
After the collisions between A and B and B and C there will be a second collision between A and B if:
One is stationary and the other is travelling towards it
Both are travelling in opposite directions towards each other
Both are travelling in the same direction and the one in front is slower than the one behind
The process is similar if object C is a wall
After B collides with the wall its direction will be reversed so it will be travelling towards A
B will collide with A again if its velocity in that direction is greater than the velocity of A in that direction (or if A was also travelling towards the wall after the first collision!)
To help you work out the speed of B after hitting the wall you will be given extra information such as the impulse exerted by the wall or the coefficient of restitution
How do I solve collisions questions involving distance and time?
As momentum problems always deal with velocities, there may also be questions that involve distances, and times
In between the collisions in collisions questions we are dealing with constant speed, so there is no need to use the suvat equations
We can instead make use of
or its rearrangements of
and
In these types of questions, the distances and/or times will usually be algebraic
e.g. "The collision between A and B takes place a distance d from the wall"
A calculator can still be used to help with any complicated fractions, just remember to account for the algebraic term afterwards
e.g.
can be found for
by finding
on your calculator, and then the answer would be
Keeping track of where the objects are, and when, in these problems is key
Draw a diagram for each stage
Use different letters for the final velocities of each stage e.g. v, and then w
Label distances on the diagrams
A common mistake after two objects collide, is forgetting that they are both moving
e.g. If A and B collide, and then B goes on to collide with a wall, and rebounds to strike A again
A will no longer be in the location where A and B collided; it will have moved whilst B was travelling to the wall
To find how far A has moved, the time for B to reach the wall would need to be found first
This could then be used in conjunction with A's speed, to find how far it has moved in this time
A common scenario in a part of these problems is when two objects at speeds
and
are approaching each other, a distance
apart
They will cover distance
, moving closer to each other at a rate of
, this can be used to find a time for when they collide
The distance between the objects will reduce in proportion to their speeds
e.g. If
and
then the ratio of distance covered will be
So they will meet at a point
from A's starting point
Examiner Tips and Tricks
These questions can be difficult to visualise in your head so draw simple diagrams to show each collision.
Use common sense, and think how many possible (or impossible) ways there are for objects to move after the first collision. You will often have to consider the speed of one or more objects to decide if a second or third collision is possible.
These questions can involve lots of algebra, negatives and inequalities so do not rush them as you might make a silly mistake which can affect subsequent parts.
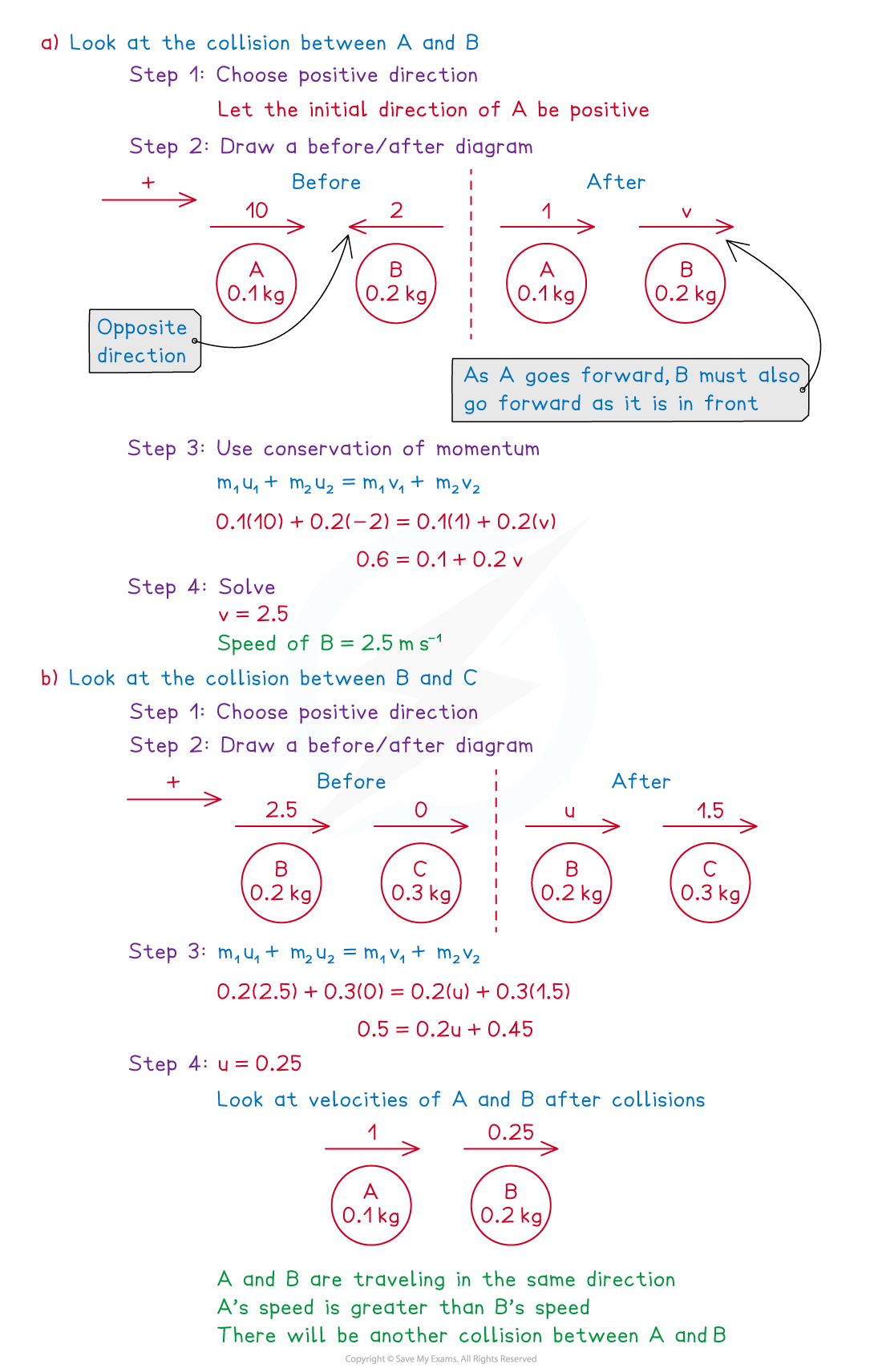
Worked Example
Three uniform balls and
of equal radius, and mass 0.1 kg, 0.2 kg and 0.3 kg respectively, can move along the same straight line on a smooth horizontal table with
in the middle of
and
.
and
are projected towards each other in opposite directions with speed
and
respectively while
is at rest.
and
collide directly which does not change the direction of motion of
and subsequently
moves with speed
.
a) Show that the speed of immediately after it collides with
is
.
b) In the subsequent motion, collides directly with
. Immediately after this collision,
moves with speed
. Determine if there will be a second collision between
and
.
Worked Example
Particles P and Q have masses 2kg and 3kg respectively. Initially they are moving in the same direction along the same straight line, such that the speed of particle P is and the speed of particle Q is
. The two particles collide when they are at a distance d from a smooth fixed vertical wall, which is perpendicular to their direction of motion. After the collision with P, particle Q collides directly with the wall and rebounds so that there is a second collision between P and Q. This second collision takes place at a distance x from the wall.
Given that the coefficient of restitution between P and Q is 1, and the coefficient of restitution between Q and the wall is 0.5, find x in terms of d.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?