Quick Sort (OCR A Level Computer Science)

Quick sort

What is a Quick Sort?

• Quick sort is another example of a divide and conquer algorithm that reduces the size of the problem into smaller problems that are more easily solvable by an algorithm

• Unlike the merge sort however, quick sort does not use any additional storage

• Below is an illustration of the quick sort

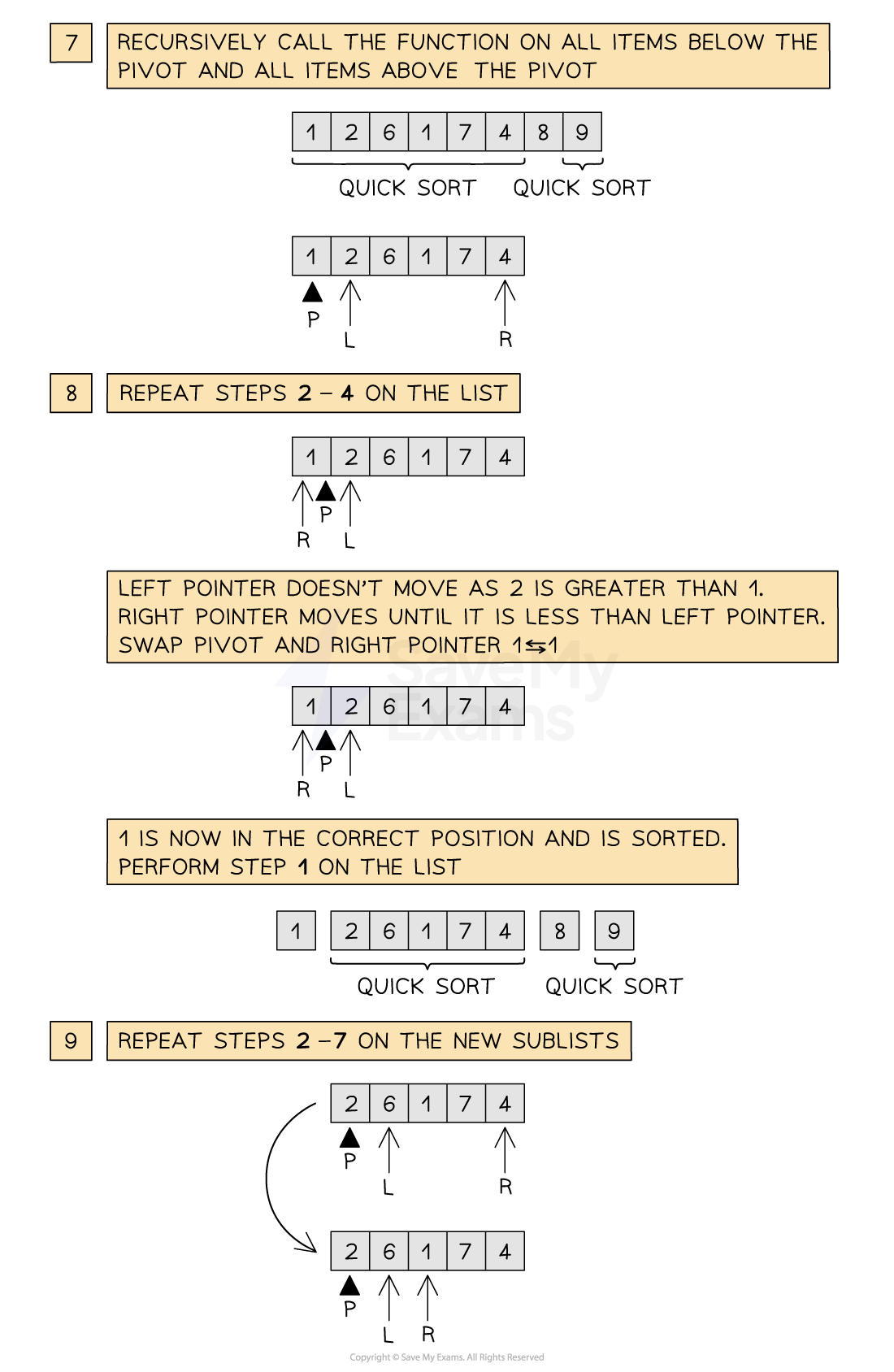
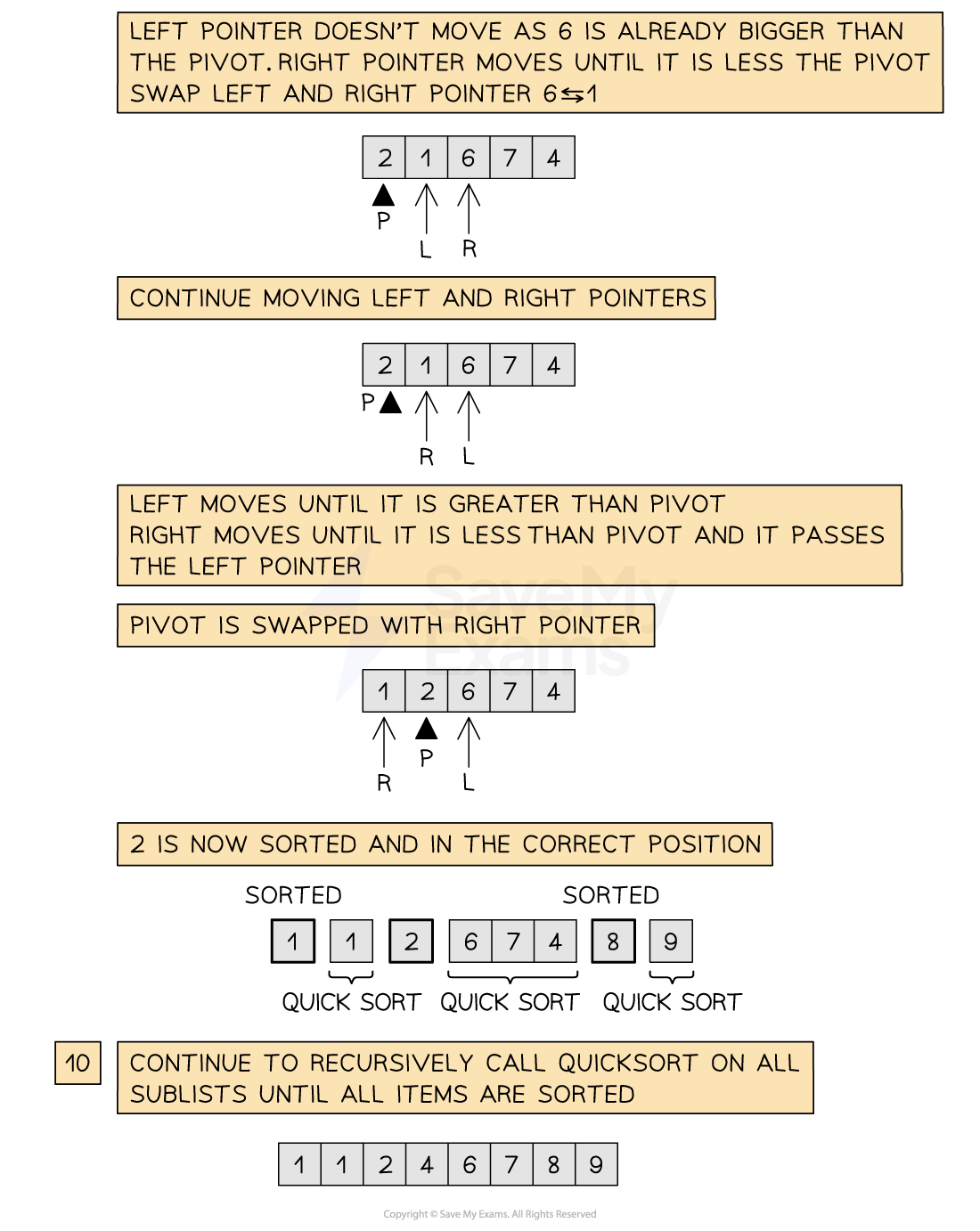
Figure 2: Performing the Quick sort

Time Complexity of a Quick Sort

• Like merge sort, quick sort is a divide and conquer algorithm which means the problem size is reduced, creating an easier problem to solve. This gives quick sort a time complexity of O(logn). Like merge sort it must sort n lists, giving it an overall best case time complexity of O(nlogn)

• Unlike merge sort, quick sort has a worst case time complexity of O(n²). This is due to the potential placement of the pivot values 

  • If the pivot value is placed roughly in the middle of the list, then quick sort performs optimally 

  • If the pivot is sorted at the start of the list, all items are above this value. If the pivot is sorted at the end of the list, all items are below this value

  • As the sorted pivots are at the extremes of the list this means there is only one call to quick sort rather than two, as no second sublist exists past the extreme. Each subsequent list has a size of n-1 with n operations performed, leading to n*(n-1) or O(n²)

  • Quick sort also has the problem that if the list is too large or pivots aren’t optimally chosen and recursion continues for too long, this can cause a stack overflow as too many stack frames have been placed on the stack

Space Complexity of a Quick Sort

• Quick sort requires additional memory as copies of lists are made and put on the stack.  The overall space complexity is therefore O(n) with O(n) additional space required

Tracing a Quick Sort

• The trace table below shows the process of calling the quick sort and moving the left and right pointers up and down the list to find elements to swap and then find the correct position of the pivot

• Once the pivot is in place, quick sort is recursively called on both sublists on either side of the pivot. Note that a second call to quick sort may not exist if the pivot value ends on either extreme of the list

• The process repeats, calling quick sort on progressively smaller sublists until all values are in the correct order

Trace Table for the Quick sort

Implementing a Quick Sort

Pseudocode 

function quicksort(list, start, end)

	if start <= end then
		return
	else
		pivot = list[start]
		left = start + 1
		right = end
		done = False
		while done == False
			while left <= right and list[left] <= pivot
				left = left + 1
			endwhile
			
			while right >= left and list[right] >= pivot
				right = right - 1
			endwhile

			if left < right then
				temp = list[left]
				list[left] = list[right]
				list[right] = temp
			else
				done = True
			endif
		endwhile

		temp = items[start]
		list[start] = list[right]
		list[right] = temp

		quicksort(list, start, right - 1)
		quicksort(list, right + 1, end)
	endif

	return list
endfunction

• The quick sort works in several stages

  • 1) The pivot is set to the 0th element, the left pointer is set to the 1st element and the right pointer is set to the end of the list

  • 2) The left pointer increments while it is less than or equal to the right pointer and the value indexed by the left pointer is less than or equal to the pivot value. Once the left pointer finds a value bigger than the pivot, or it passes the right pointer it stops

  • 3) After the left pointer has been incremented, the right pointer is decremented. While the right pointer is greater than or equal to the left pointer and the value indexed by the right pointer is greater than or equal to the pivot value, the right pointer is decremented

  • 4) If both pointers have not yet passed each other but both have finished moving, the values indexed by both pointers are swapped. The pointers then continue moving as per step 2 and 3

  • 5) If both pointers pass each other then the swapping is done. The pivot value is then swapped with the value indexed by the right pointer. The pivot value is now in the correct position and is sorted

  • 6) Both sides of the pivot value now exist as two new sublists. Quicksort is recursively called on both sublists and the process repeats as per step 1

  • 7) Steps 1-7 repeat until all sublists have been sorted

Python

def quicksort(data, start, end):
  if start <= end:
    pivot = data[start]
    left = start + 1
    right = end
    done = False
    while not done:
      while left <= right and data[left] <= pivot:
        left += 1
      while right >= left and data[right] >= pivot:
        right -= 1
      if left < right:
        temp = data[left]
        data[left] = data[right]
        data[right] = temp
      else:
        done = True
    temp = data[start]
    data[start] = data[right]
    data[right] = temp
    quicksort(data, start, right - 1)
    quicksort(data, right + 1, end)
  return data

data = [5, 2, 7, 4, 9, 10, 1, 8, 3]
quicksort(data, 0, len(data) - 1)
print(data)  # Output: [1, 2, 3, 4, 5, 7, 8, 9, 10]

Java

public class QuickSort {

    public static void quickSort(int[] data, int start, int end) {
        if (start < end) {
            int pivotIndex = partition(data, start, end);
            quickSort(data, start, pivotIndex - 1);
            quickSort(data, pivotIndex + 1, end);
        }
    }

    private static int partition(int[] data, int start, int end) {
        int pivot = data[start];
        int left = start + 1;
        int right = end;
        while (true) {
            while (left <= right && data[left] <= pivot) {
                left++;
            }
            while (right >= left && data[right] >= pivot) {
                right--;
            }
            if (left < right) {
                swap(data, left, right);
            } else {
                break;
            }
        }
        swap(data, start, right);
        return right;
    }

    private static void swap(int[] data, int i, int j) {
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }

    public static void main(String[] args) {
        int[] data = {5, 2, 7, 4, 9, 10, 1, 8, 3};
        quickSort(data, 0, data.length - 1);
        System.out.println(Arrays.toString(data));  // Output: [1, 2, 3, 4, 5, 7, 8, 9, 10]
    }
}