Dijkstra's Shortest Path Algorithm (OCR A Level Computer Science): Revision Note
Exam code: H446
Dijkstra’s Shortest Path Algorithm
What is Dijkstra's shortest path algorithm?
In A Level Computer Science, Dijkstra's shortest path algorithm is an example of an optimisation algorithm that calculates the shortest path from a starting location to all other locations
Dijkstra’s uses a weighted graph in a similar manner to a breadth first search to exhaust all possible routes to find the optimal route to the destination node
To revise Graphs you can follow this link
Each route is represented as an arc/edge from a node/vertex. Each edge carries a weighted value which represents some measurement, for example time, distance or cost
An illustrated example of Dijkstra's is shown below
What is an optimisation problem?
Optimisation problems involve maximising the efficiency of a solution to solve the stated problem. Examples of optimisation problems can include:
Finding the shortest route between two points. This is used for planning journeys, creating networks, building circuit boards, etc.
Minimising resource usage in manufacturing or games
Timetabling lessons in school or office meetings
Scheduling staff breaks and work hours
The most common optimisation problem encountered in daily life is finding the shortest route from A to B. Various apps exist to calculate these distances, such as Google Maps or road trip planners
Performing Dijkstra's shortest path algorithm
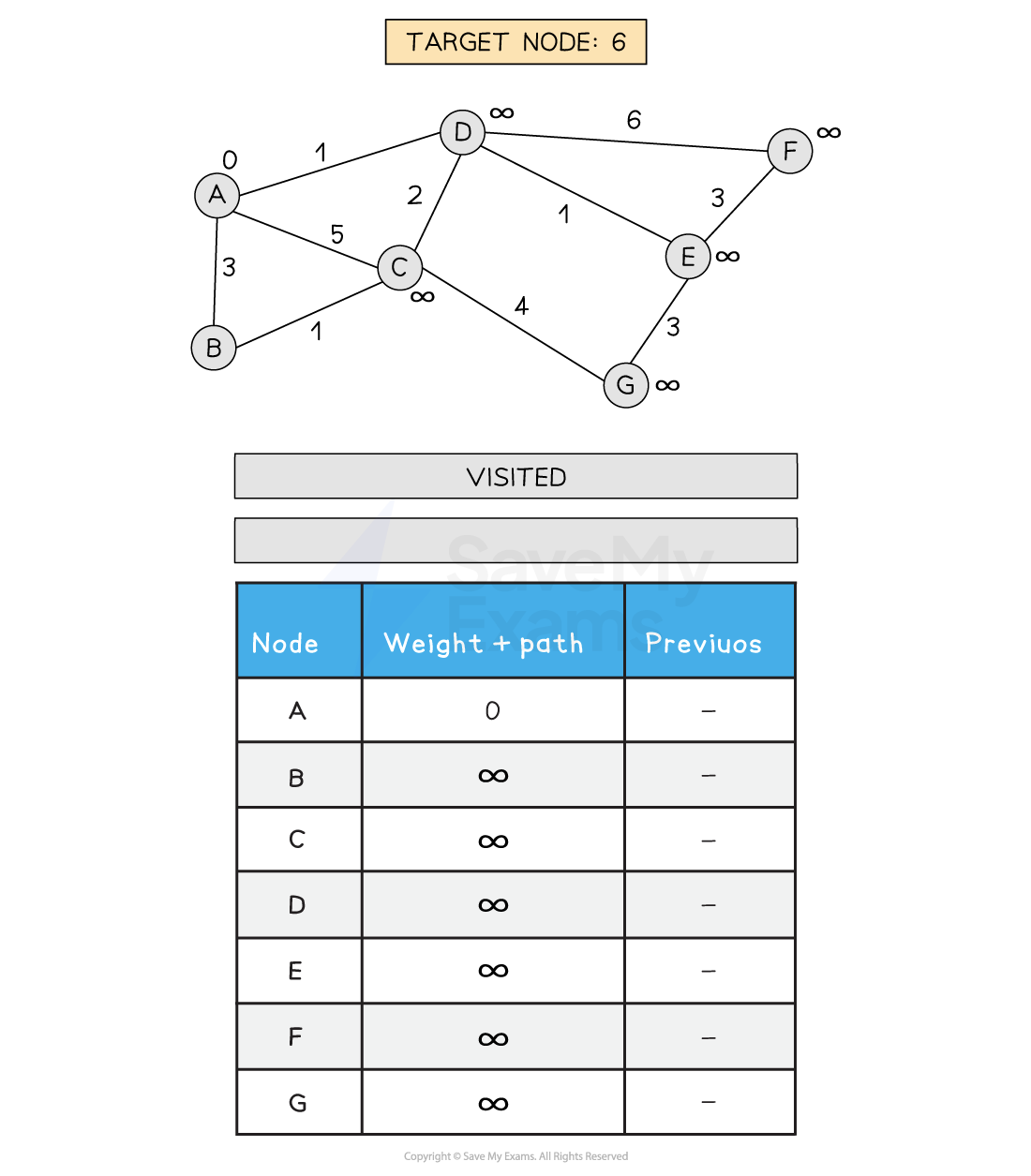
1) Set A path to 0 and all other path weights to infinity
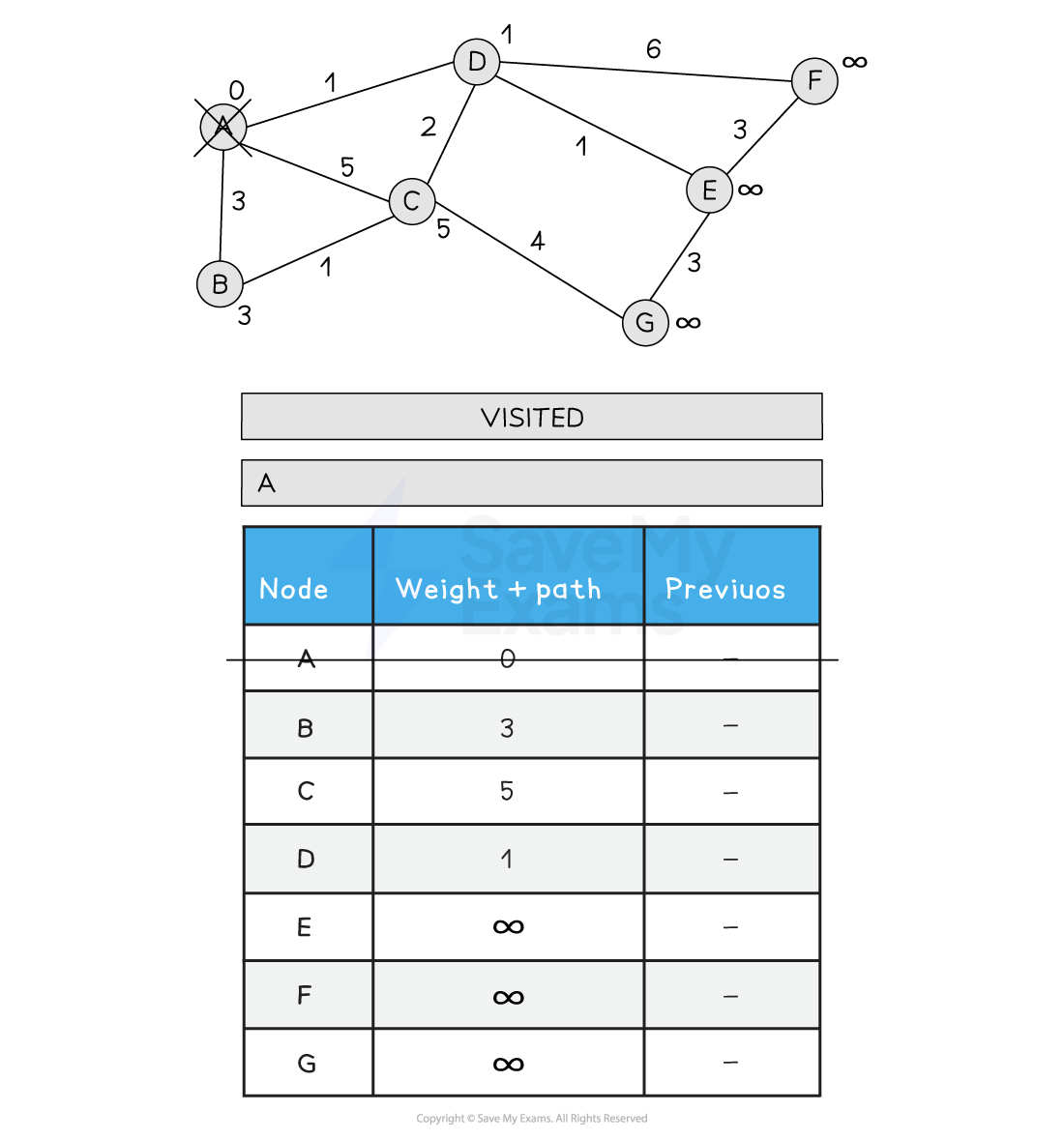
2) Visit A. Update all neighbouring nodes path weights to the distance from A + A's path weight (0)
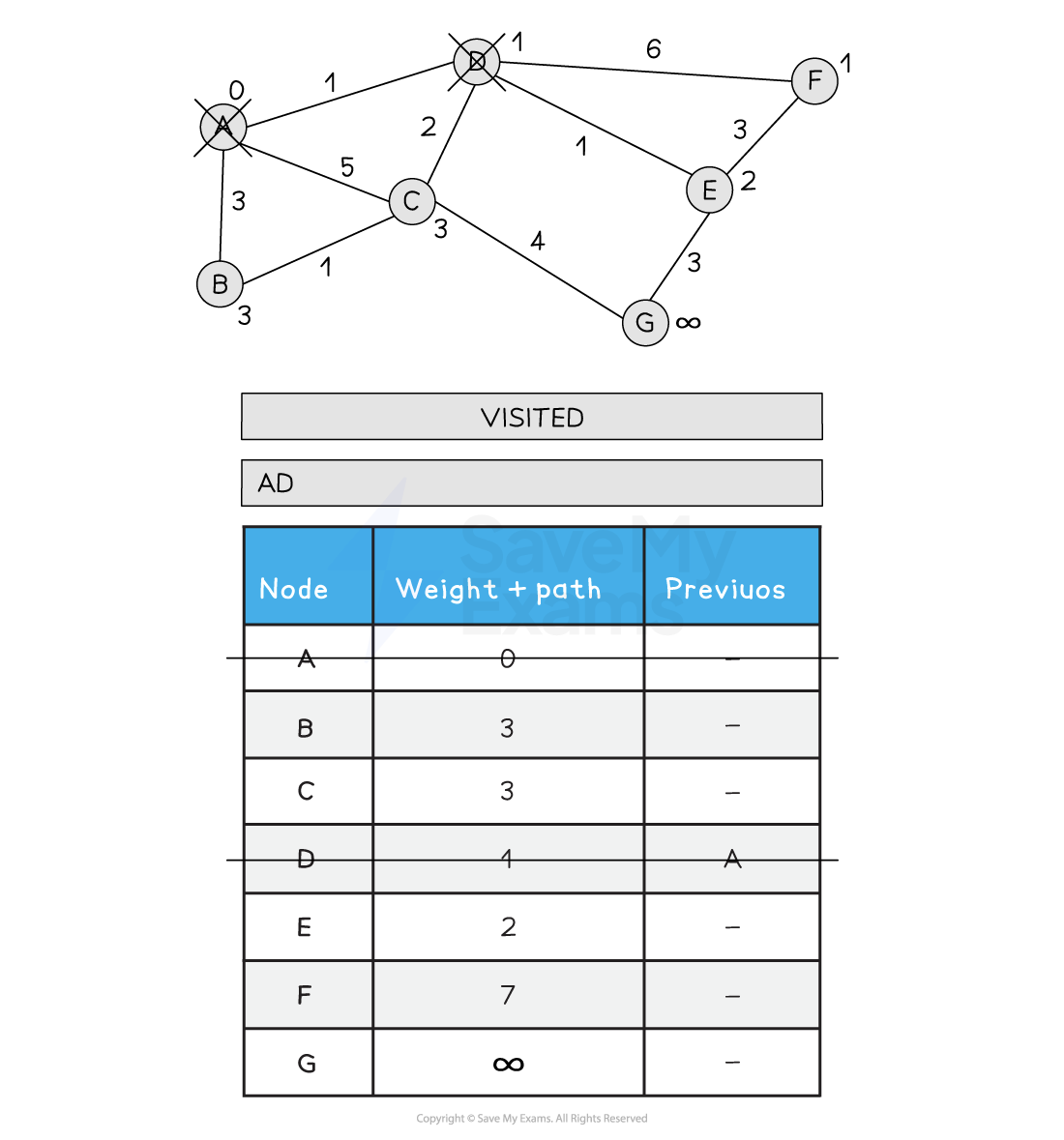
3) Choose the next node to visit that has the lowest path weight (D). Visit D. Update all neighbouring, non-visited nodes with a new path weight if the old path weight is bigger than the new path weight. C is updated from 5 to 3 as the new path is shorted (A > D > C)
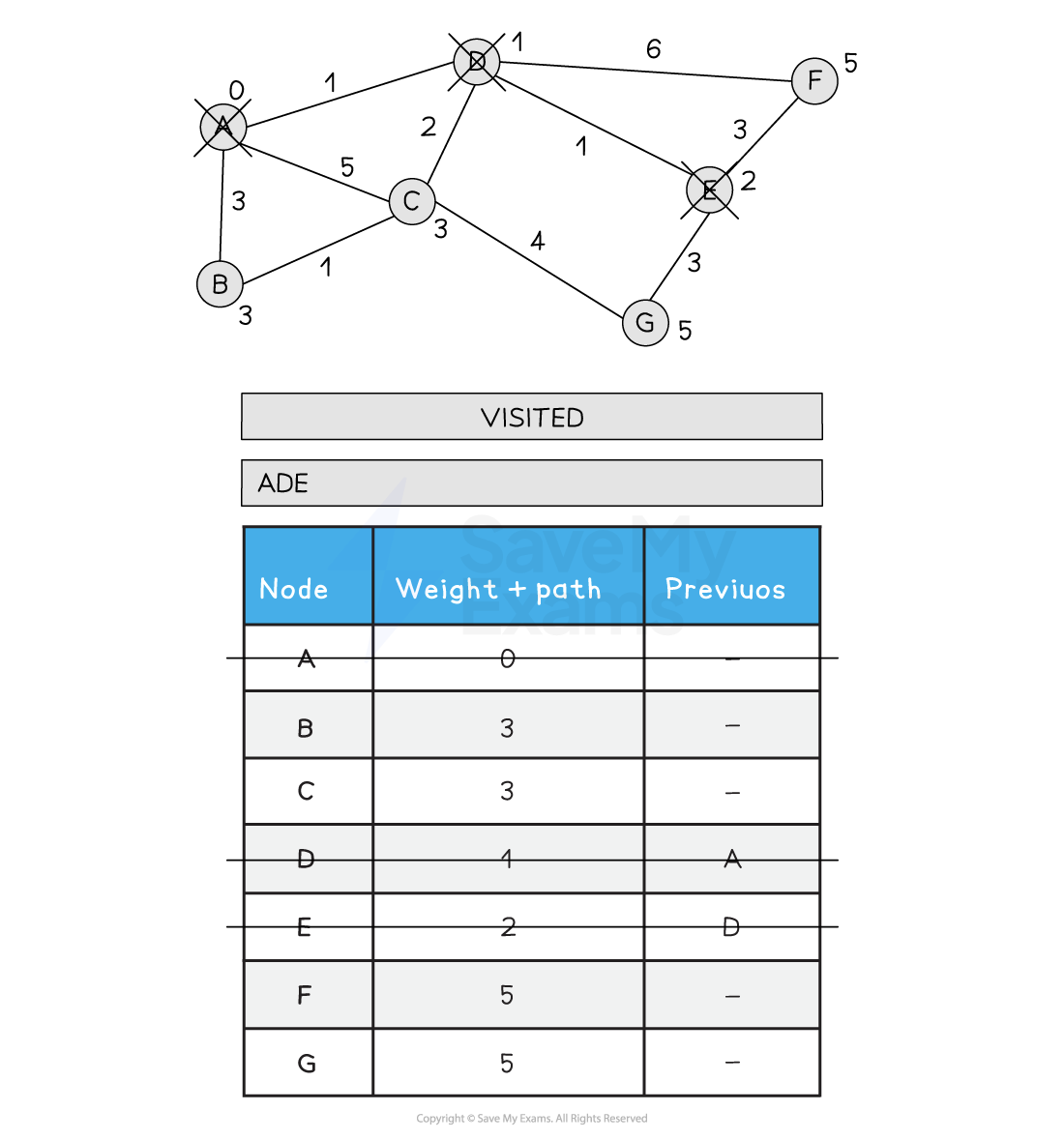
4) Choose the next node to visit that has the lowest path weight (E). Visit E. Update all neighbouring, non-visited nodes from E with a new path weight. F is updated from 7 to 5 as the new path is shorter (A > D > E > F)
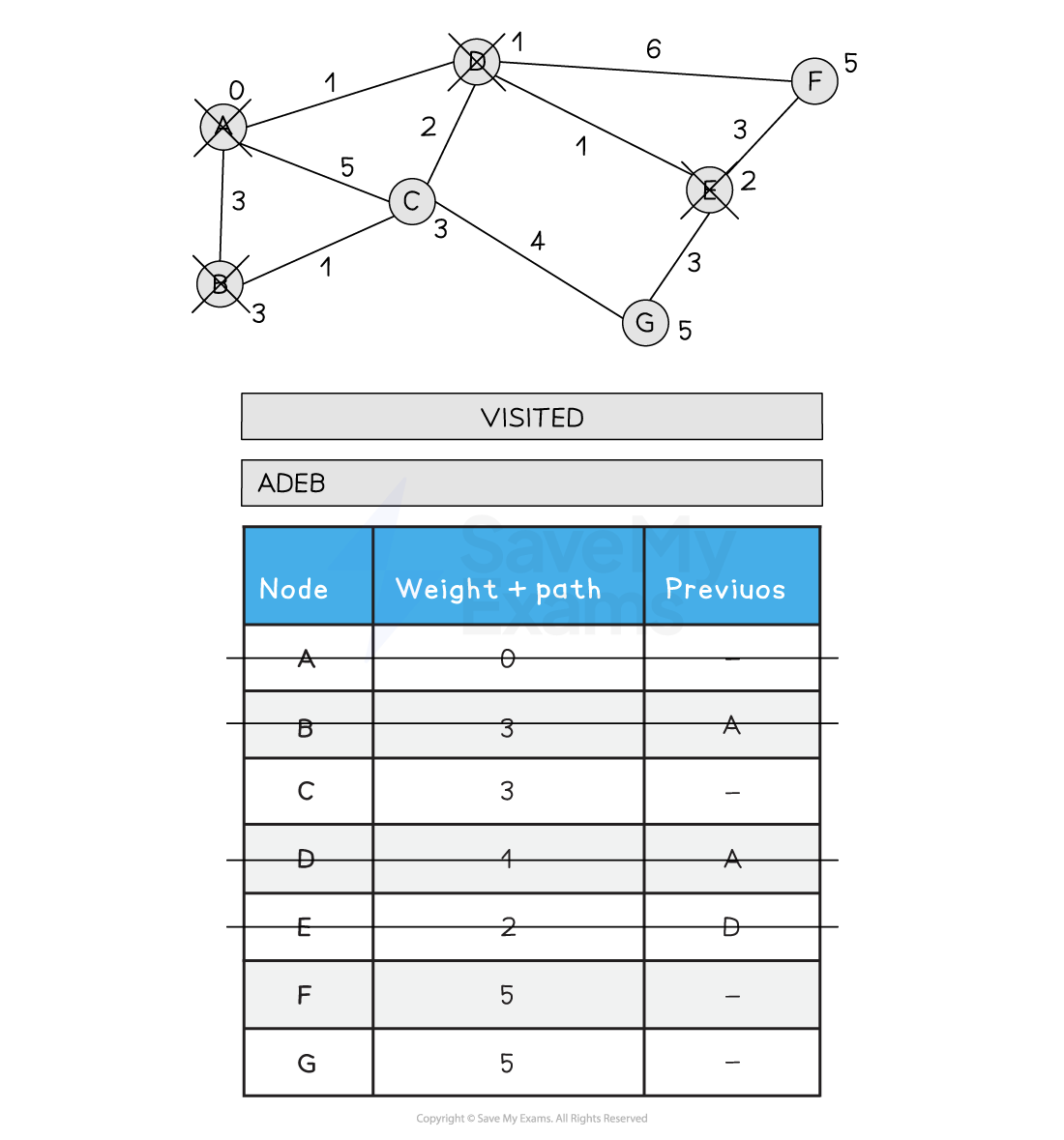
5) Choose the next node to visit, alphabetically (B). Visit B. Update all neighbouring non-visited nodes from B with a new weight if the path is less than the current path. C is not updated as A > B > C is 4
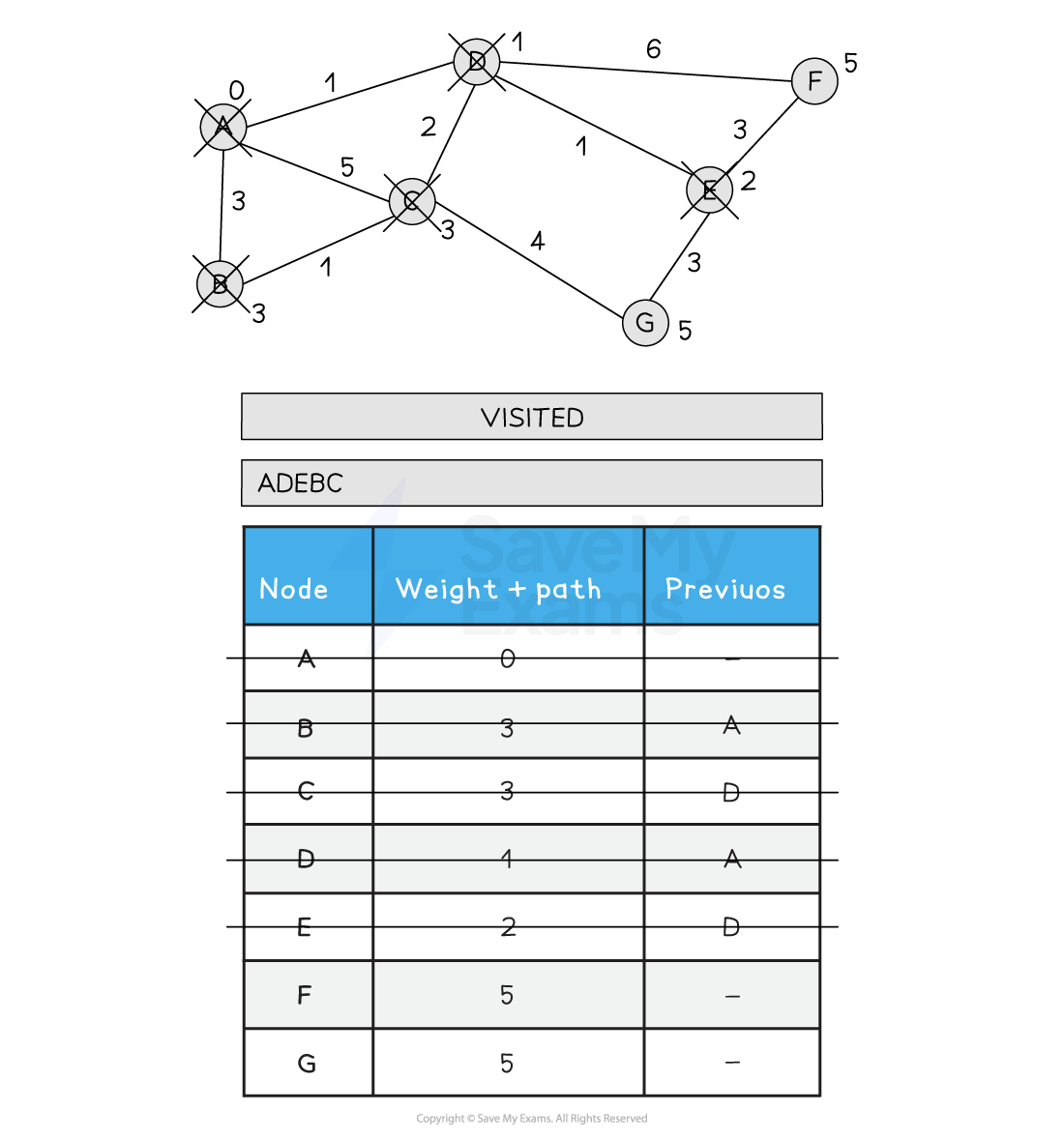
6) Choose the next lowest node and visit (C). Update C's neighbours if the new path is shorter than the old path. A > D > C > G is 8, so G is not updated
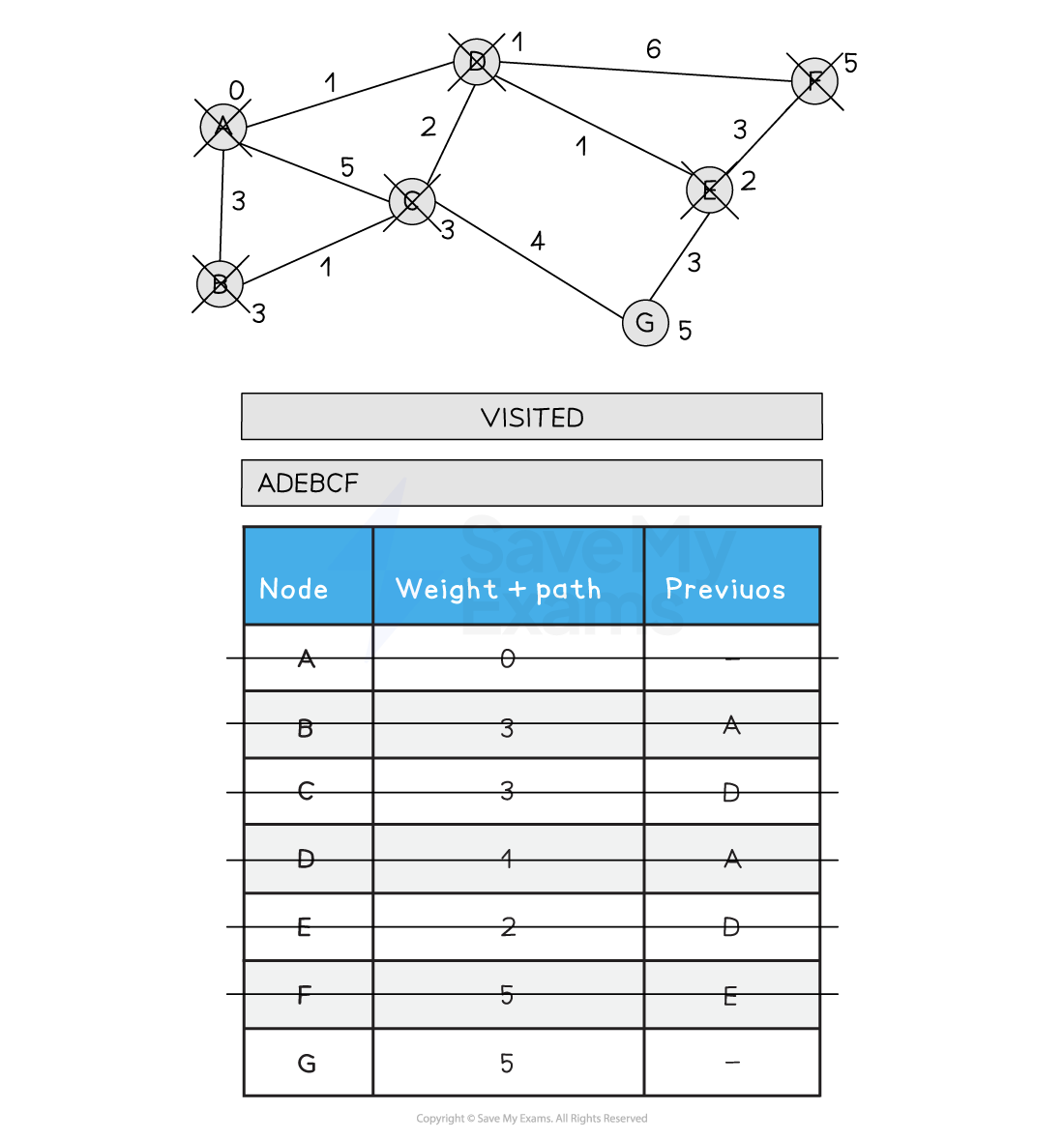
7) Choose the next lowest node and visit (F). Update F's neighbours if the new path is shorter than the old path. F has no non-visited neighbours so no updates are made
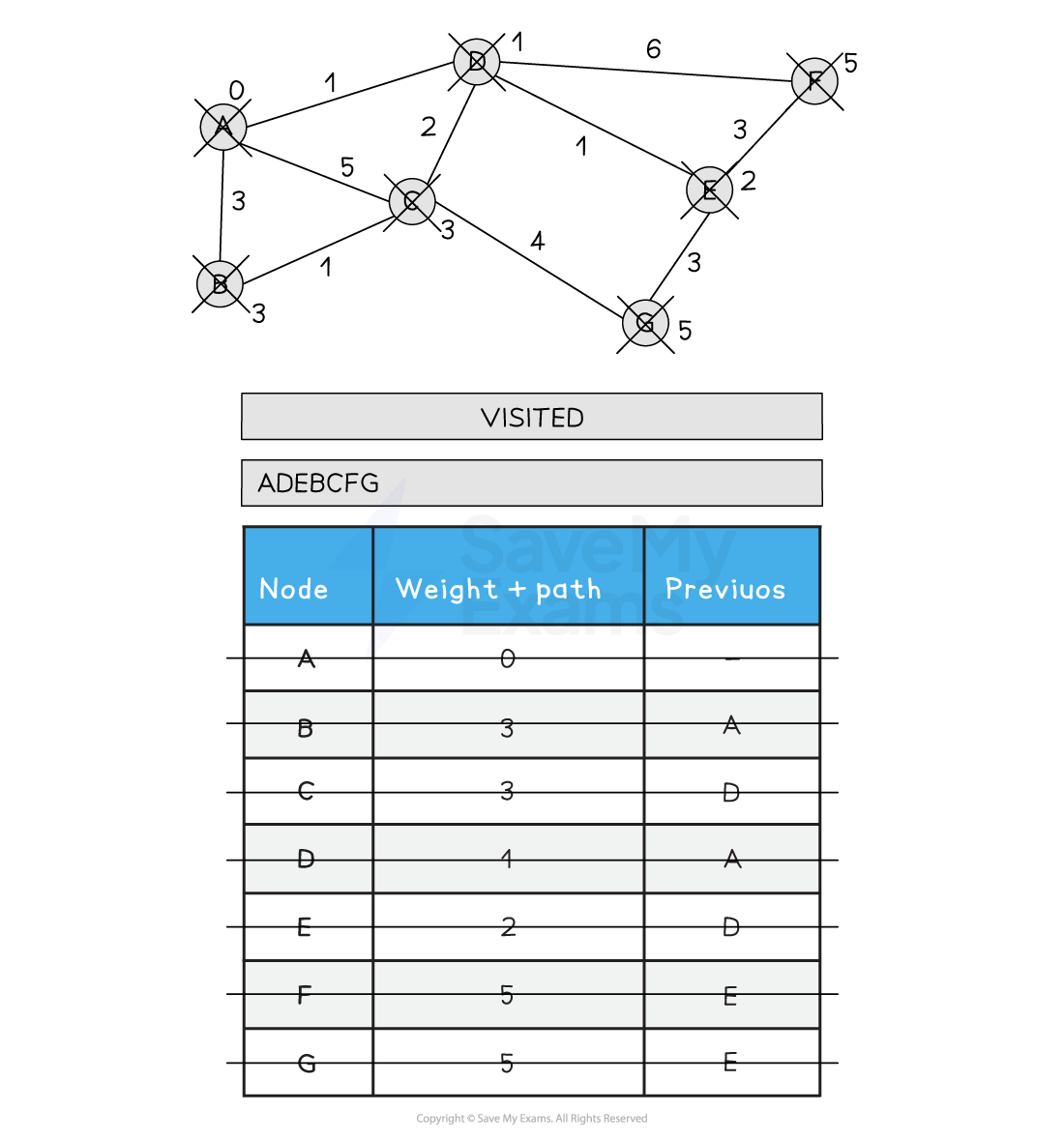
8) Choose the next lowest node and visit (G). G has no non-visited neighbours so no updates are made
9) All nodes have been visited. Back tracking from G gives the following order and total distance A-D-E-G (5)
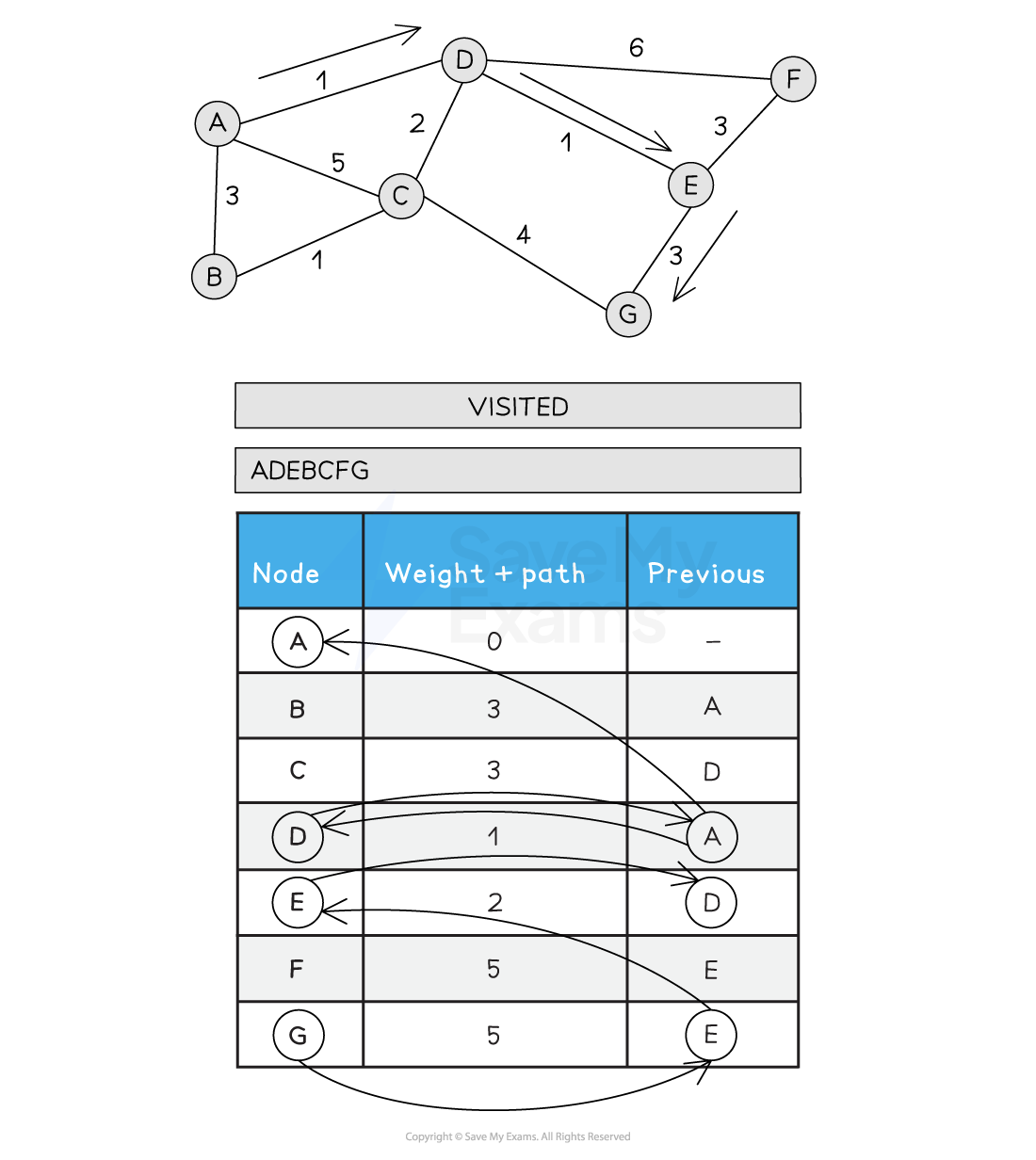
Figure 1: Performing Dijkstra’s Shortest path Algorithm
The algorithm for Dijkstra's is shown below, both in structured English and a pseudocode format
Dijkstra’s shortest path algorithm (structured English)
assign a distance value of 0 to the initial node and infinity for every other node
add all nodes to a priority queue, sorted by current distance
while the queue is not empty
remove node x from the front of the queue and add to a visited list
for each unvisited neighbour y of the current node x
newDistance = distanceAtX + distanceFromXtoY
if newDistance < distanceAtY then
distanceAtY = newDistance
reorder the priority queue by changing Y’s position based on the new distance
endif
next X
endwhileDijkstra’s shortest path algorithm (Pseudocode)
function Dijkstra(graph, start, goal)
//set all distances to infinity and first distance to 0
for node in graph
distance[node] = infinity
next node
distance[start] = 0
while unvisitedNodes in graph
//find the shortest distance from all the nodes in order to select the next node to visit and expand
min = null
for node in graph
if min == null then
min = node
elseif distance[node] < distance[min] then
min = node
endif
next node
//for each neighbour, update the cost if the current cost and distance are less than the previously stored distance
for neighbour in graph
if cost + distance[min] < distance[neighbour] then
distance[neighbour] = cost + distance[min]
previousNode[neighbour] = min
endif
next neighbour
visited.append(node)
endwhile
//backtrack through the previous nodes and build up the final path until the start is reached
node = goal
while node != start
path.append(node)
node = previousNode[node]
endwhile
return path
endfunctionExaminer Tips and Tricks
You will not be asked to program Dijkstra's in the exam as the algorithm is too complex to implement. You may be asked about parts of the algorithm however
In the first above algorithm, a priority queue is used to order the nodes in terms of distance The shortest routes are prioritized to be explored next. In the second algorithm above, a simple loop finds the next shortest node in the list. Both are valid methods
Once a node has been removed from the queue it is added to a visited list and is not rechecked
It is important to note that the algorithm is exhaustive and will check every available node and path, calculating the shortest distance from the initial node to every other node
As Dijkstra’s is a graph traversal algorithm, a dictionary storing the nodes and neighbours will need to be passed to the algorithm
A corresponding dictionary of distances from the starting node to each node will also need to be kept during the algorithm
Examiner Tips and Tricks
You do not need to know the time or space complexity for Dijkstra's shortest path algorithm
Tracing Dijkstra's Shortest path Algorithm
Tracing Dijkstra's shortest path algorithm can be done in a manner similar to Figure 1 above
Remember to initialise the starting node to 0 and all other nodes to infinity
Update each nodes neighbours by adding the previous path and the distance from the current node to the neighbour
Keep track of each nodes previous node that offered the shortest route
Worked Example
Mabel is a software engineer. She is writing a computer game for a client. In the game the main character has to avoid their enemies. This becomes more difficult as the levels of the game increase.
The game’s ‘challenging’ level has intelligent enemies that hunt down the character in an attempt to stop the user from winning. The program plans the enemies’ moves in advance to identify the most efficient way to stop the user from winning the game.
The possible moves are shown in a graph. Each node represents a different state in the game. The lines represent the number of moves it will take to get to that state.
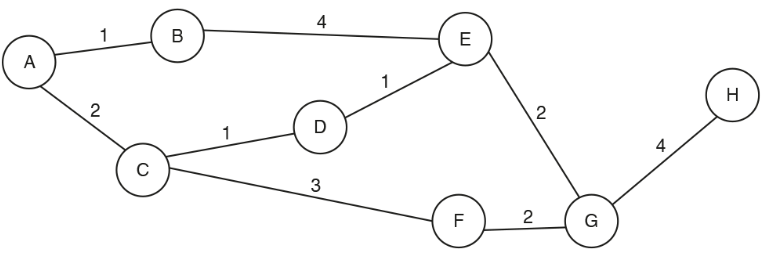
Show how Dijkstra’s algorithm would find the shortest path from A to H.
6 marks
Node | Visited | From A | Previous Node |
|
|---|---|---|---|---|
A | ✓ | 0 | - | [1] |
B | ✓ | 1 | A | [1] |
C | ✓ | 2 | A | |
D | ✓ | 3 | C | [1] |
F | ✓ | 5 | C | |
E | ✓ | 5 4 | B D | [1] |
G | ✓ | 6 | E | [1] |
H |
| 10 | G |
|
Final route: ACDEGH (length 10) [1]
Only one mark is available for the final route. Remember to show your working. You won’t get given the table in the exam, just lots of lines but you can draw a table like the one above

Unlock more, it's free!
Did this page help you?