Binary Search (OCR A Level Computer Science)

Binary Search

What is a Binary Search?

• The binary search is a more efficient search method than linear search

• The binary search compares the middle item to the searched for target item. If the values match then the index is returned. If not then the list is adjusted such that:

  •  the top half is ignored if the target item is less than the middle value

  • or the bottom half is ignored if the target item is larger than the middle value

• Once the list has been adjusted, the search continues until the item is found or the item is not in the list

• It is important to note that the list must be sorted for the binary search to work correctly

• The implementation of the binary search is shown below

Performing the Binary Search

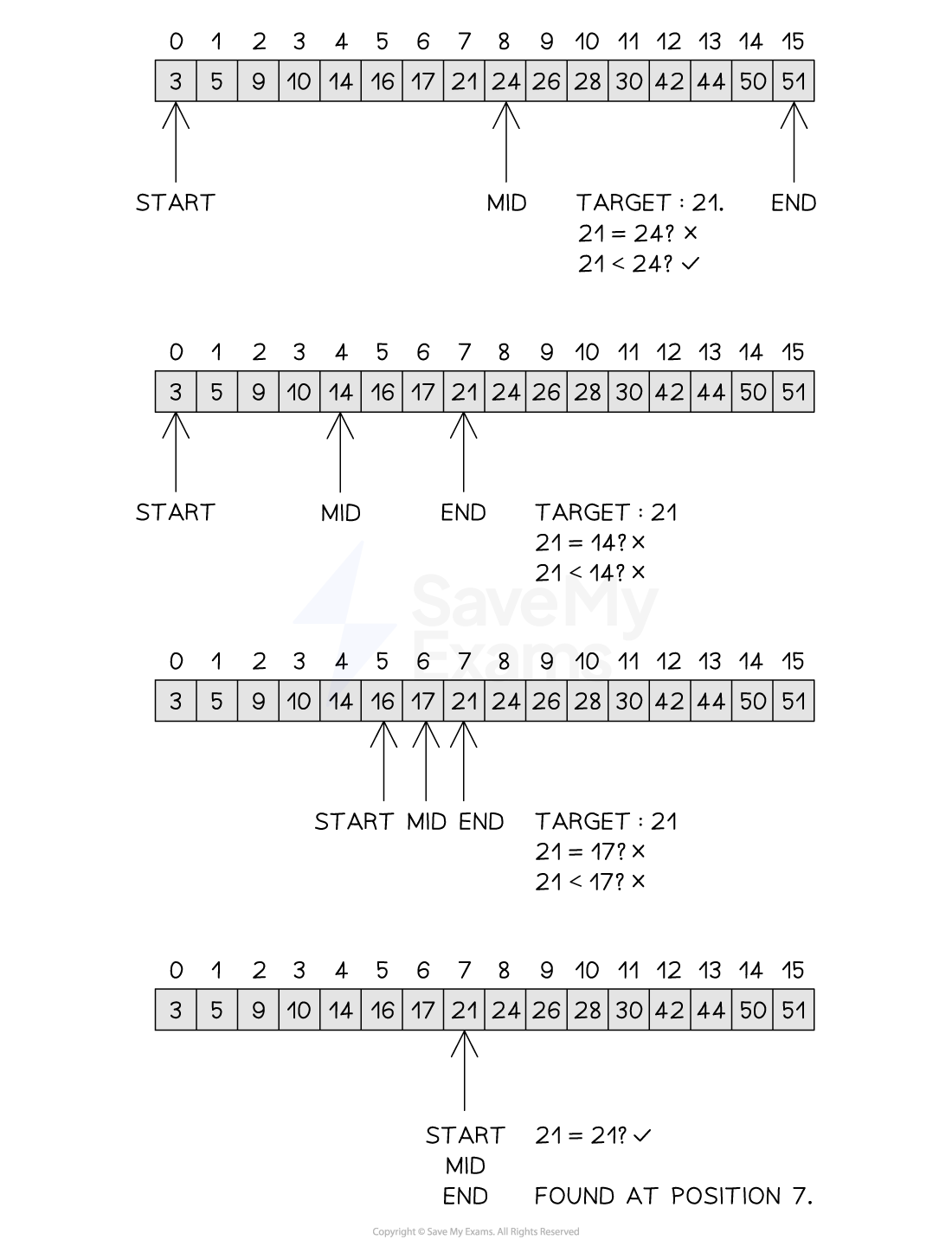
Figure 2: Performing the Binary Search

Time Complexity of a Binary Search

• The binary search is an example of a logarithmic time complexity O(logn) as it halves the search space with each iteration of the while loop. This approach is known as divide and conquer, where a problem is progressively reduced in size such that when each problem is at its smallest it is easiest to solve

• The algorithm starts with n items before the first iteration. After the first there are n/2 items, after the second there are n/4 items, after the third there are n/8 items and so on, leading to n/2ⁱ after i iterations

• The worst case scenario or maximum number of iterations to find one item is where n/2ⁱ = 1

  • Multiply both sides by 2ⁱ to get: n = 2ⁱ

  • Take the logarithm of both sides: logn = log2ⁱ

  • Rewrite with i at the front (using laws of logarithms): logn = ilog2

  • Log2 (assuming a base of 2 is used) becomes 1, giving: logn = i

  • The binary search is therefore O(logn)

• The best case scenario would be O(1) where the item is found on the first comparison, while the average case would be O(logn/2) which would find the item somewhere in the middle of the search. Removing coefficients means the average case would therefore still be O(logn)

Space Complexity of a Binary Search

• As the binary search requires no additional space, it is space complexity O(n), where n is the number of items in the list

Tracing a Binary Search

• Given the following list [3, 5, 9, 10, 14, 16, 17, 21, 24, 26, 28, 30, 42, 44, 50, 51], a trace table for the binary search is shown below

Trace Table for the Binary Search

Implementing a Binary Search

Pseudocode

function binarySearch(list, item)
  found = False
  index = -1
  start = 0
  end = len(list - 1)
  while start <= last and found = False
    mid = round(start + end) / 2
    if list[mid] = item then
      found = True
      index = mid
    else
      if list[mid] < item then
        start = mid + 1
      else
        last = mid - 1
      endif
    endif
  endwhile
  return index
endfunction

• In the above algorithm, a list of n ordered items is passed to the function and three pointer values are set to the start element list[0], the mid element list[n/2], and the last element list[n-1] 

• Each pointer is an integer value, with the midpoint being rounded up to the next whole number. These pointers are used to index the list

• With each iteration of the while loop, the mid value is compared against the item being looked for. If it is the same then the item is found and the index returned 

• If it is not the same then the algorithm checks to see if it is smaller or bigger than the item being looked for. If it is bigger then the start pointer is adjusted and moved to just after the mid pointer, otherwise the end pointer is adjusted and moved to just under the mid pointer

• This gives the illusion of the list shrinking in size and allows the algorithm to narrow in on the true location of the item with each iteration. If the item is not found, -1 is returned

Python

def binary_search(list, item):
  found = False
  index = -1
  start = 0
  end = len(list) - 1

  while start <= end and not found:
    mid = (start + end) // 2
  if list[mid] == item:
    found = True
    index = mid
  elif list[mid] < item:
    start = mid + 1
  else:
    end = mid - 1

  return index

Java

public class BinarySearch {

    public static int binarySearch(int[] list, int item) {
        boolean found = false;
        int index = -1;
        int start = 0;
        int end = list.length - 1;

        while (start <= end && !found) {  // Corrected found condition
            int mid = (start + end) / 2;

            if (list[mid] == item) {
                found = true;
                index = mid;
            } else if (list[mid] < item) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }

        return index;
    }