A* Algorithm (OCR A Level Computer Science) : Revision Note
A* Search Algorithm
What is an A* search algorithm?
In A Level Computer Science, the A* algorithm builds on Dijkstra’s by using a heuristic
A heuristic is a rule of thumb, best guess or estimate that helps the algorithm accurately approximate the shortest path to each node
Dijkstra’s shortest path algorithm is an example of a path-finding algorithm. Other path finding algorithms exist that are more efficient. One example is the A* search
Dijkstra’s uses a single cost function i.e. the weight of the current path plus the total weight of the path so far. This is the real distance from the initial node to every other node
To revise Graphs you can follow this link
The cost function is unreliable, for example, going from node A to B may be a large distance such as 117, whereas going from A to C may be a distance of 5. Dijkstra’s will follow node C even if it doesn’t lead to the goal node as A to C is simply the shortest path
In order to prevent going in the wrong direction, another function is necessary: a heuristic function
A* search uses g(x) as the real distance cost function and h(x) as the heuristic function
Every node will have a heuristic value. The purpose of the heuristic function is that it will approximate the Euclidean distance i.e. the straight line distance from the current node to the goal node. By following nodes based on shorter heuristic distances, the algorithm can be sure it is getting closer to the goal node
As the heuristic is an estimate, it is not necessarily optimum. The A* search operates under the assumption that the heuristic function should never overestimate the real cost from the initial node to the goal node. The real cost should always be greater or equal to the heuristic function
The total cost f(x) of each node rather than just g(x) (the distance from node X to Y plus the previous route total distance) is g(x) + h(x) (the estimate of how far the goal node is away from the current node)
The calculation for each node is therefore f(x) = g(x) + h(x)
If h(x) increases compared to the previous node, it means the algorithm is traveling further away from the goal node
A* search focuses on reaching the goal node unlike Dijkstra’s which calculates the distance from the initial node to every other node
Below is an illustration of the A* search
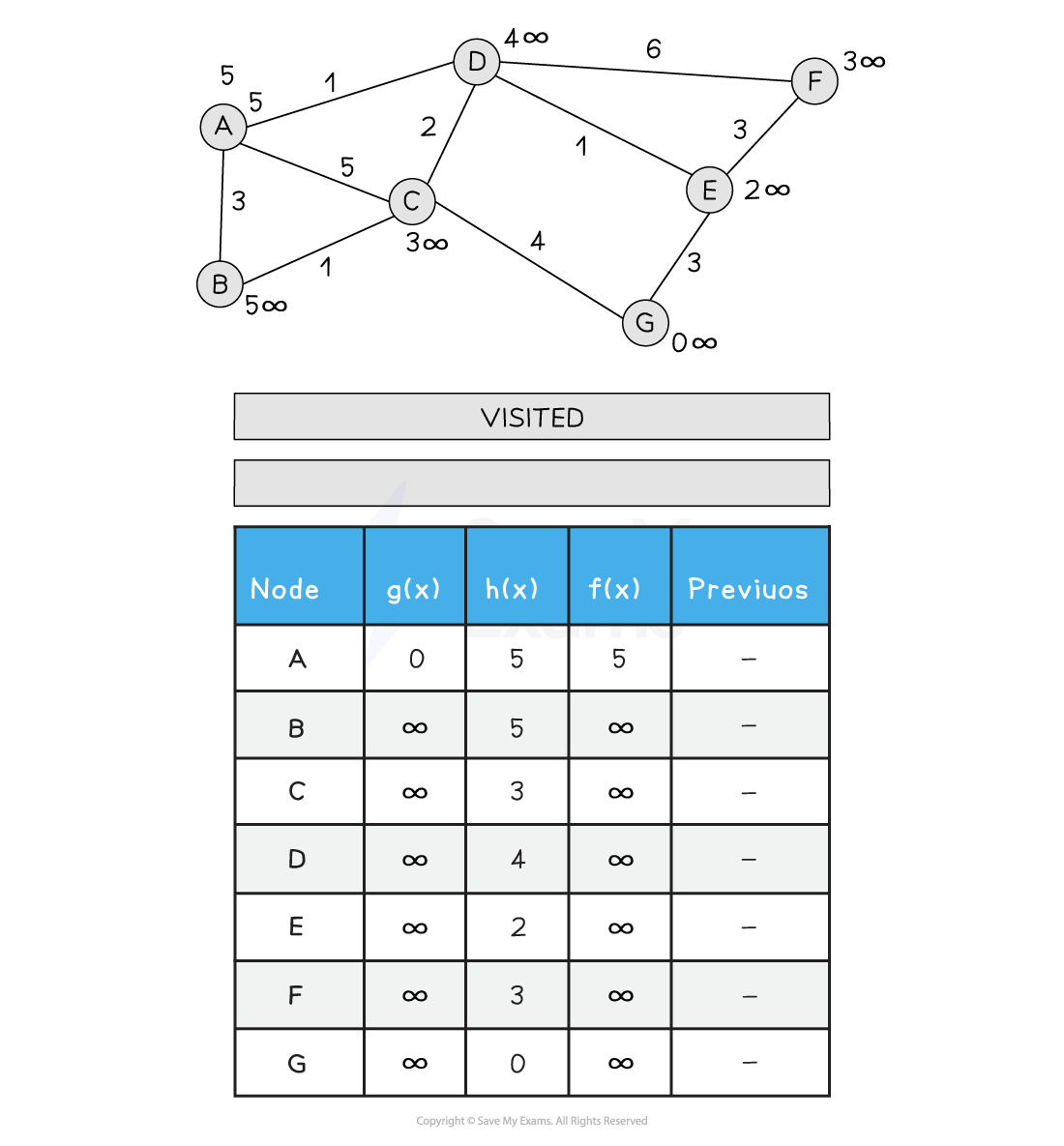
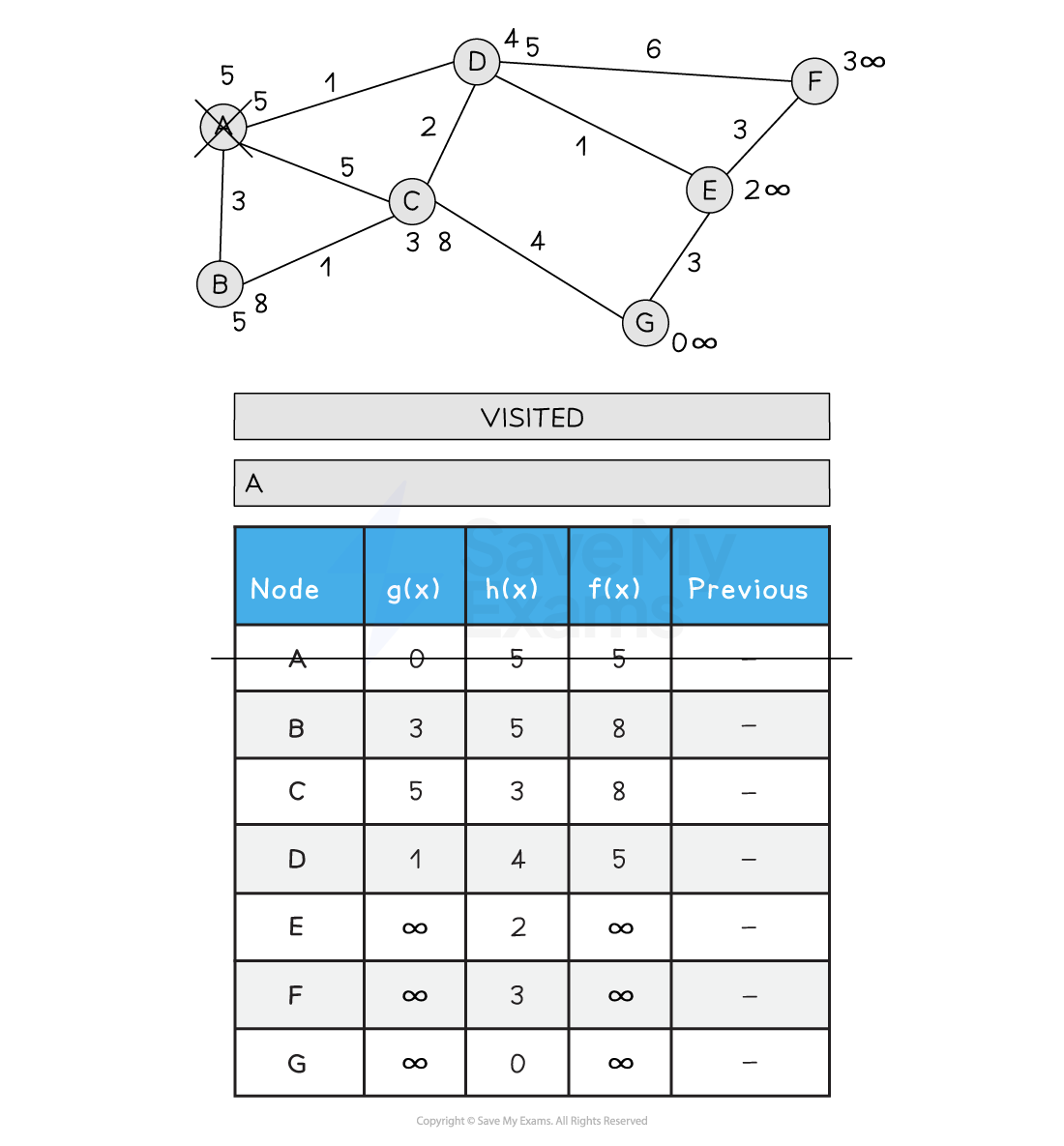
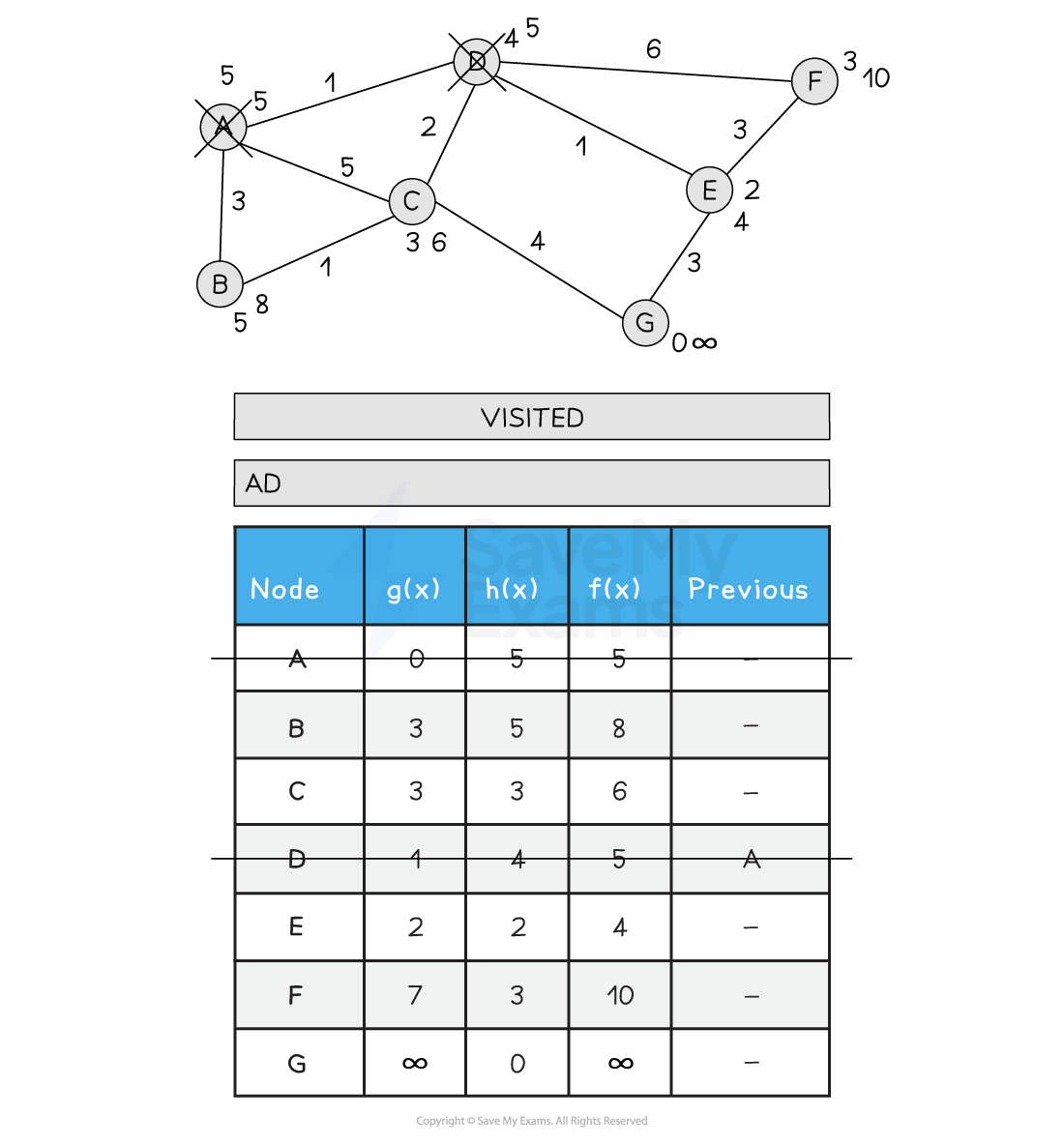
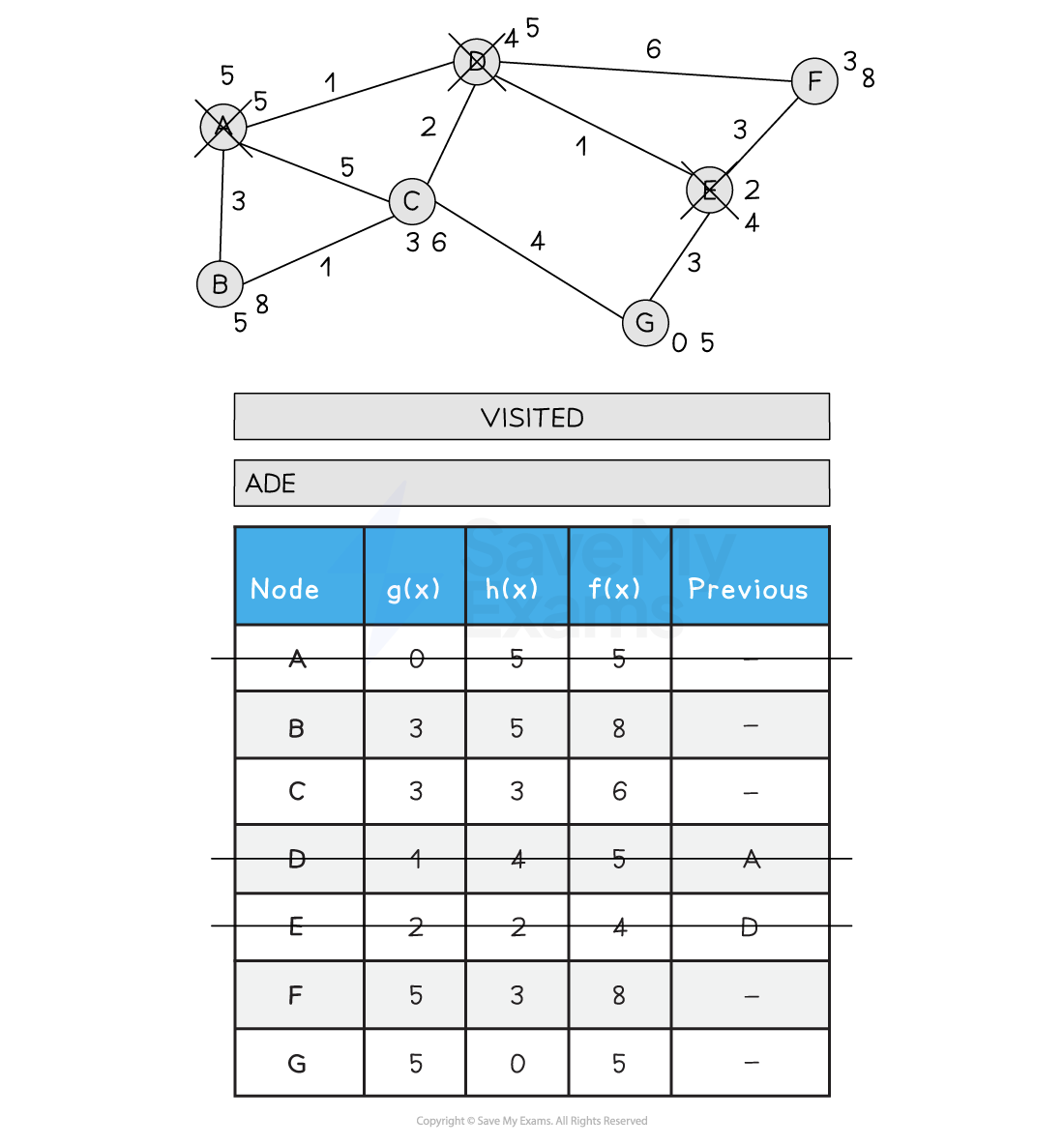
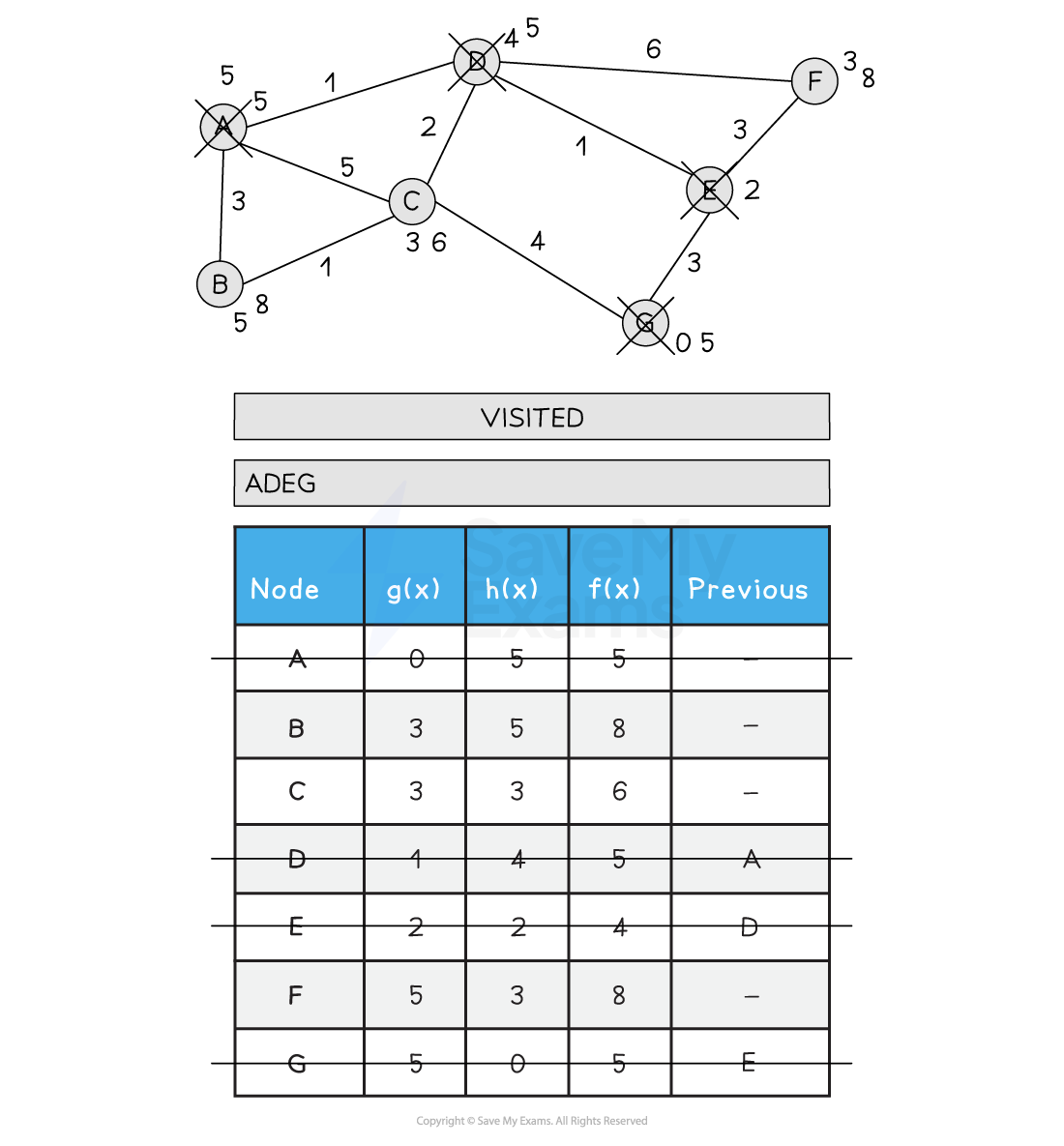
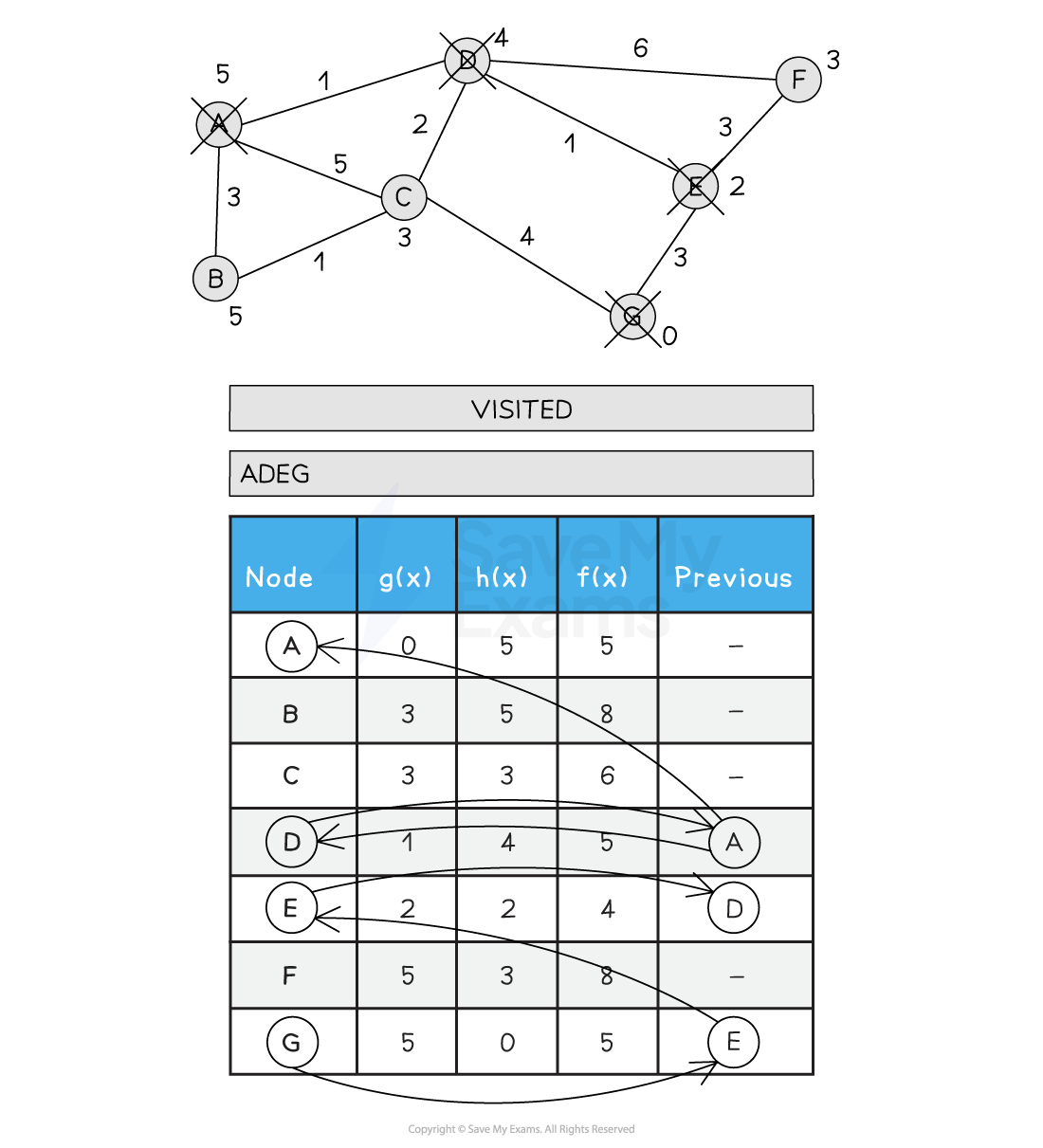
Figure 2: Performing the A* Search
The algorithm for A* search is shown below, both in structured english and a pseudocode format
A* Search (Structured English)
assign g(x) to 0 and f(x) to h(x) for the initial node and g(x) and f(x) to infinity for every other node
add all nodes to a priority queue, sorted by f(x)
while the queue is not empty
remove node x from the front of the queue and add to a visited list
If node x is the goal node,
end the while loop
else
for each unvisited neighbour y of the current node x
g(x) = g(x)AtX + distanceFromXtoY
if g(x) < g(x)AtY then
g(x)AtY = g(x)
f(x)AtY = g(x)AtY + h(x)AtY
reorder the priority queue by changing Y’s position based on the new f(x)
endif
next X
endwhile
A* Search (Pseudocode)
function AStarSearch(graph, start, goal)
//set all distances to infinity and first distance to 0
for node in graph
g[node] = infinity
f[node ] infinity
next node
g[start] = 0
f[start] = h[start]
//A* ends when the goal node has been reached
while goal in graph
//find the shortest distance f(x) from all the nodes in order to select the next node to visit and expand
min = null
for node in graph
If min == null then
min = node
elseif f[node] < f[min] then
min = node
endif
next node
//for each neighbour, update the cost if the current cost and distance are less than the previously stored distance
for neighbour in graph
if cost + distance[min] < distance[neighbour] then
distance[neighbour] = cost + distance[min]
F[neighbour] = cost + g[min] + h[neighbour]
previousNode[neighbour] = min
endif
next neighbour
graph.remove(min)
endwhile
//backtrack through the previous nodes and build up the final path until the start is reached
node = goal
while node != start
path.append(node)
node = previousNode[node]
endwhile
return path
endfunctionA* search behaves almost exactly as Dijsktra’s except that when the goal node is reached, the algorithm stops and the old cost function is replaced with a new heuristic based function
Examiner Tips and Tricks
You do not need to know the time or space complexity for the A* search algorithm
Tracing the A* Search Algorithm
Tracing the A* search algorithm can be done in a manner similar to the Figure 2 above
Remember to initialise the starting node g(x) to 0 and f(x) to h(x)
Update each nodes neighbours by adding the previous path and the distance from the current node to the neighbour to the heuristic value for the neighbour node
Keep track of each nodes previous node that offered the shortest route
Worked Example
Some of the characters in a game will move and interact independently. Taylor is going to use graphs to plan the movements that each character can take within the game.
DancerGold is one character. The graph shown in Fig. 1 shows the possible movements that DancerGold can make.
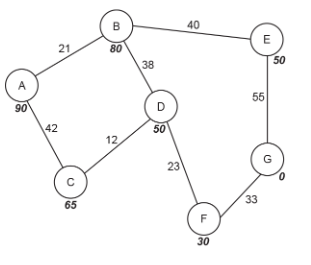
Fig. 1
DancerGold’s starting state is represented by node A. DancerGold can take any of the paths to reach the end state represented by node G.
The number on each path represents the number of seconds each movement takes.
The number in bold below each node is the heuristic value from A.
i) Define the term heuristic in relation to the A* algorithm.
2 marks
ii) Perform an A* algorithm on the graph shown in Fig. 1 to find the shortest path from the starting node to the end node. Show your working, the nodes visited and the distance. You may choose to use the table below to give your answer.
Node | Distance travelled | Heuristic | Distance travelled + Heuristic | Previous node |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Final path:
Distance:
8 marks
Answer:
i) An heuristic is a rule of thumb or guess [1] that estimates the distance or cost from one node to the destination node [1].
ii)
|
Final path = A,C,D,F,G and Distance = 110 [1]
Remember that the distance travelled is based on the edge weights between two nodes. This is added to the heuristic to find the total distance travelled to a node.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?