Ionic Product of Water (Edexcel A Level Chemistry)

• In all aqueous solutions, an equilibrium exists in water where a few water molecules dissociate into protons and hydroxide ions
• We can derive an equilibrium constant for the reaction:

• This is a specific equilibrium constant called the ionic product for water
• The product of the two ion concentrations is always 1 x 10^-14 mol² dm^-6
• This makes it straightforward to see the relationship between the two concentrations and the nature of the solution:

[H⁺] & [OH^–] Table

The relationship between K_w and pK_w is given by the following equation:

pK_w = -logK_w

pK_a

• The range of values of K_a is very large and for weak acids, the values themselves are very small numbers

Table of K_a values

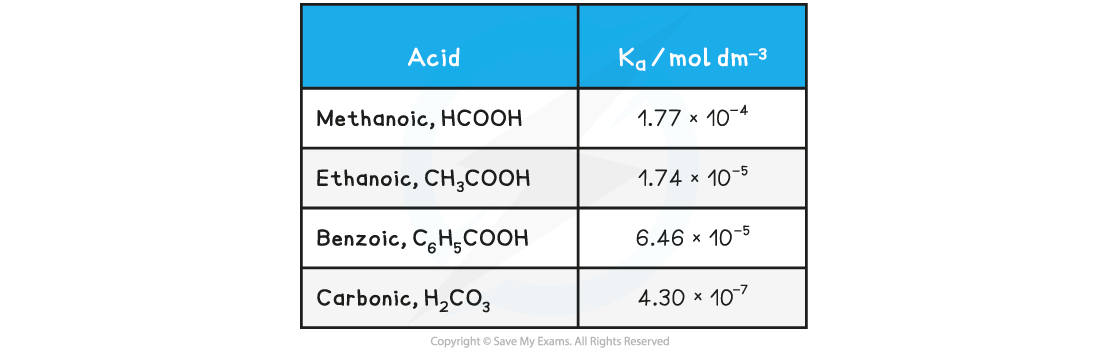
• For this reason it is easier to work with another term called pK_a
• The pK_a  is the negative log of the K_a value, so the concept is analogous to converting [H⁺] into pH values

pK_a = -logK_a

• Looking at the pK_a values for the same acids:

Table of pK_a values

• The range of pK_a values for most weak acids lies between 3 and 7

• Strong bases are completely ionised in solution

BOH (aq) → B⁺ (aq) + OH^- (aq)

• Therefore, the concentration of hydroxide ions [OH^-] is equal to the concentration of base [BOH]
  • Even strong alkalis have small amounts of H⁺ in solution which is due to the ionisation of water
• The concentration of OH^- in solution can be used to calculate the pH using the ionic product of water
• Once the [H⁺] has been determined, the pH of the strong alkali can be founding using pH = -log[H⁺]

• Similarly, the ionic product of water can be used to find the concentration of OH^- ions in solution if [H⁺] is known, simply by dividing K_w by the [H⁺]

Answer

Sodium hydroxide is a strong base which ionises as follows:

NaOH (aq) → Na⁺ (aq) + OH^- (aq) 

Answer 1:

   The pH of the solution is:

   [H⁺] = K_w  ÷ [OH^-]

   [H⁺] = (1 x 10^-14) ÷ 0.15 = 6.66 x 10^-14

   pH = -log[H⁺]

         = -log 6.66 x 10^-14  = 13.17

Answer 2

Step 1: Calculate hydrogen concentration by rearranging the equation for pH

   pH = -log[H⁺]

   [H⁺]= 10^-pH

   [H⁺]= 10^-10.50

   [H⁺]= 3.16 x 10^-11 mol dm^-3

Step 2: Rearrange the ionic product of water  to find the concentration of hydroxide ions

   K_w = [H⁺] [OH^-]

    [OH^-]= K_w  ÷  [H⁺] 

Step 3: Substitute the values into the expression to find the concentration of hydroxide ions

   Since K_w is 1 x 10^-14 mol² dm^-6,

    [OH^-]= (1 x 10^-14)  ÷  (3.16 x 10^-11)

   [OH^-]= 3.16 x 10^-4 mol dm^-3