A LevelChemistryCambridge (CIE)Revision Notes5. Chemical EnergeticsHess’s LawHess’s Law

Hess’s Law (Cambridge (CIE) A Level Chemistry): Revision Note

Exam code: 9701

Caroline Carroll

Written by: Caroline Carroll

Updated on

Hess Cycles

  • Hess’s Law states that:

"The total enthalpy change in a chemical reaction is independent of the route by which the chemical reaction takes place as long as the initial and final conditions are the same."

  • This means that whether the reaction takes place in one or two steps, the total enthalpy change of the reaction will still be the same

Illustration of Hess's Law

Flowchart with three routes: direct from A+B to C, indirect route 1 via F+G, indirect route 2 via X and Y+Z. Arrows indicate direction.
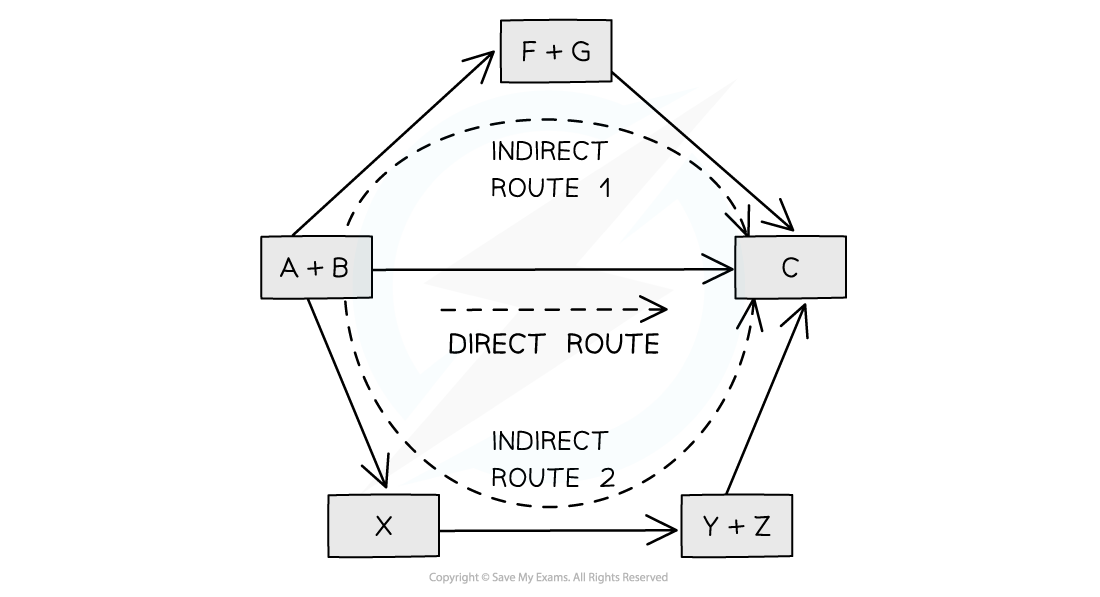
According to Hess’ Law, the enthalpy change of the direct route, going from reactants (A+B) to product (C), is equal to the enthalpy change of the indirect routes

  • Hess’ Law is used to calculate enthalpy changes which can’t be found experimentally using calorimetry, e.g.:

3C (s) + 4H2 (g) → C3H8(g)

  • ΔHf (propane) can’t be found experimentally as hydrogen and carbon don’t react under standard conditions

Calculating ΔHr from ΔHf using Hess’s Law energy cycles

  • The products can be directly formed from the elements = ΔH2 OR The products can be indirectly formed from the elements = ΔH1 + ΔHr

Applying Hess's Law

Diagram illustrating Hess's Law with rectangles labelled reactants, products, and elements, showing direct and indirect routes with enthalpy changes.
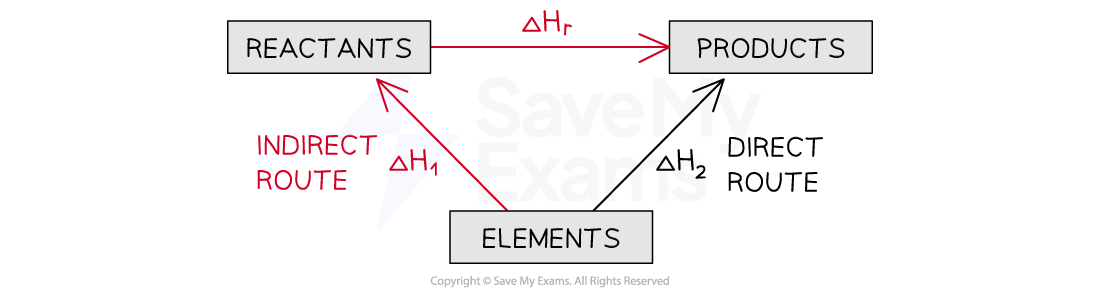
The enthalpy change from elements to products (direct route) is equal to the enthalpy change of elements forming reactants and then products (indirect route)

  • Equation

ΔH2 = ΔH1 + ΔHr

Therefore,

ΔHr = ΔH2 – ΔH1 

Worked Example

Calculate ΔHr for the following reaction:

2NaHCO3 (s) → Na2CO3 (s) + CO2 (g) + H2O (l)

The table shows the standard enthalpy of formations, ΔHθf, relevant to this reaction.

Molecule

ΔHθf kJ mol-1 

NaHCO3 (s)

–950.8

Na2CO3 (s)

–1130.7

CO2 (g)

–393.5

H2O (l)

–285.8

Answer

  • Step 1: Write the balanced equation at the top

Hess cycle step 1: the equation 2NaHCO3(s) → Na2CO3(s) + CO2(g) + H2O(l) written at the top of the cycle, reactants on the left and products on the right.

  • Step 2: Draw the cycle with the elements at the bottom

Hess cycle step 2: 2NaHCO3(s) and Na2CO3(s) + CO2(g) + H2O(l) at the top, with the elements 2Na(s) + 2C(graphite) + 3O2(g) + H2(g) drawn below them.

  • Step 3: Draw in all arrows, making sure they go in the correct directions. Write the standard enthalpy of formations

Completed Hess cycle: arrow from 2NaHCO3(s) to Na2CO3(s) + CO2(g) + H2O(l) is the enthalpy change of reaction; arrow from the elements 2Na(s) + 2C(graphite) + 3O2(g) + H2(g) up to 2NaHCO3(s) is ΔH1 = 2 x ΔHf[NaHCO3(s)]; arrow from the elements to the products is ΔH2 = ΔHf[Na2CO3(s)] + ΔHf[CO2(g)] + ΔHf[H2O(l)].

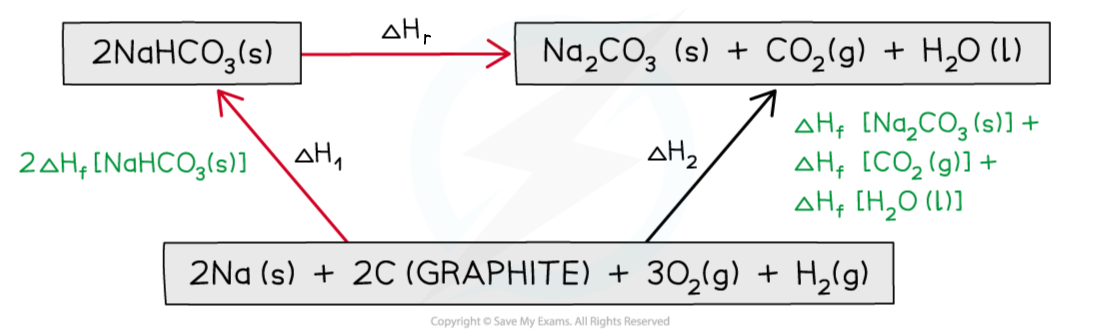
  • Step 4: Apply Hess’s Law:

    • ΔHr = ΔH2 – ΔH1

    • ΔHr = ( ΔHf [Na2CO3 (s)] + ΔHf [CO2 (g)] + ΔHf [H2O (l)] ) – 2ΔHf [NaHCO3 (s)]

    • ΔHr = ( (–1130.7) + (–393.5) + (–285.8) ) – ( 2 x –950.8)

    • ΔHr = +91.6 kJ mol-1 

Calculating ΔHf  from ΔHc using Hess’s Law energy cycles

  • The combustion products can be formed directly from elements to combustion products = ΔH1 OR The combustion products can be formed indirectly from elements to compounds to combustion products = ΔHf + ΔH2

 Hess's Law and combustion enthalpies 

Flowchart illustrating combustion: arrows connect "Elements + Oxygen," "Compound Formed + Oxygen," and "Combustion Products" with ΔH annotations.
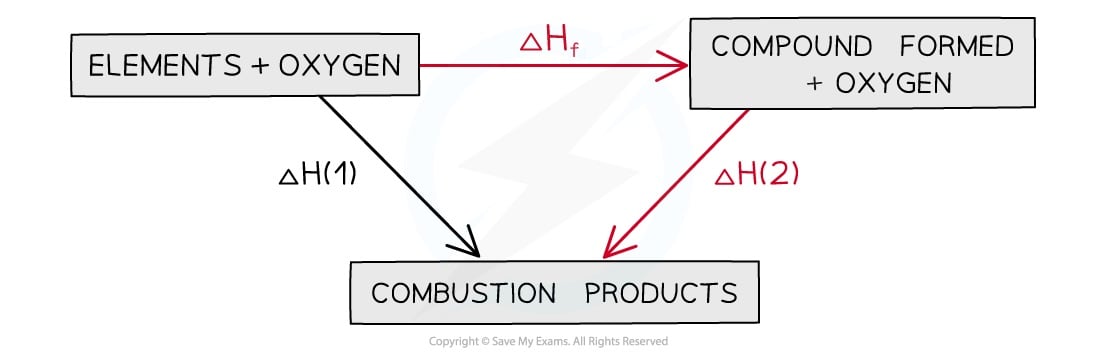
The enthalpy change going from elements to products (direct route) is equal to the enthalpy change of elements forming reactants and then products (indirect route)

  • Equation

ΔH1 = ΔHf + ΔH2

  • Therefore,

ΔHf  = ΔH1 – ΔH2

Worked Example

Calculate, using the standard enthalpy change of combustion values given, the enthalpy of formation of ethane.

Reaction

ΔHc kJ mol-1 

C (graphite) + O2 (g) → CO2 (g)

–393.5

H2 (g) + ½O2 (g) → H2O (l)

–285.8

C2H6 (g) + 3½O2 (g) → 2CO2 (g) + 3H2O (l)

–1559.7

Answer

  • Step 1: Write the equation for the enthalpy change of formation at the top and add oxygen on both sides

Combustion cycle step 1: the formation equation for ethane at the top, 2C(graphite) + 3H2(g) + 3½O2(g) → C2H6(g) + 3½O2(g), with oxygen added to both sides.

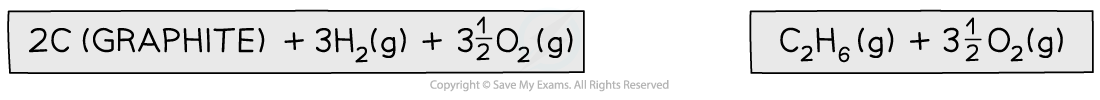
  • Step 2: Draw the cycle with the combustion products at the bottom

Combustion cycle step 2: the elements plus oxygen, 2C(graphite) + 3H2(g) + 3½O2(g), and ethane plus oxygen, C2H6(g) + 3½O2(g), at the top, with the combustion products 2CO2(g) + 3H2O(l) at the bottom.

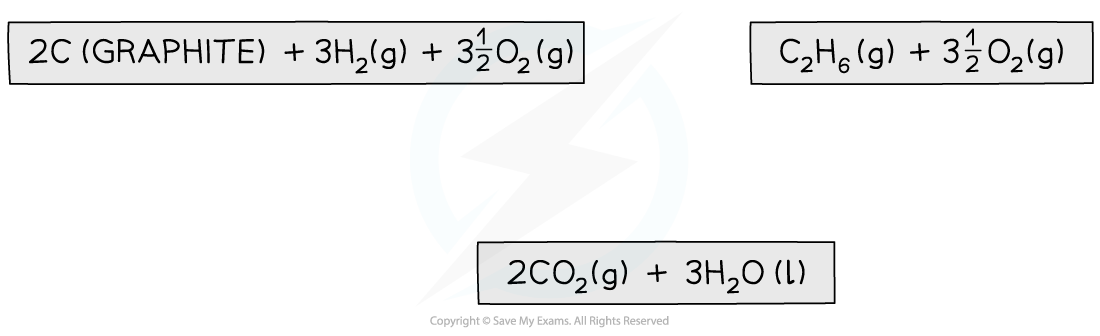
  • Step 3: Draw all arrows in the correct direction

Completed combustion cycle: ΔHf arrow from the elements plus oxygen to ethane plus oxygen; ΔH1 = 2ΔHc[C(graphite)] + 3ΔHc[H2(g)] from the elements plus oxygen down to 2CO2(g) + 3H2O(l); ΔH2 = ΔHc[C2H6(g)] from ethane plus oxygen down to the same products.

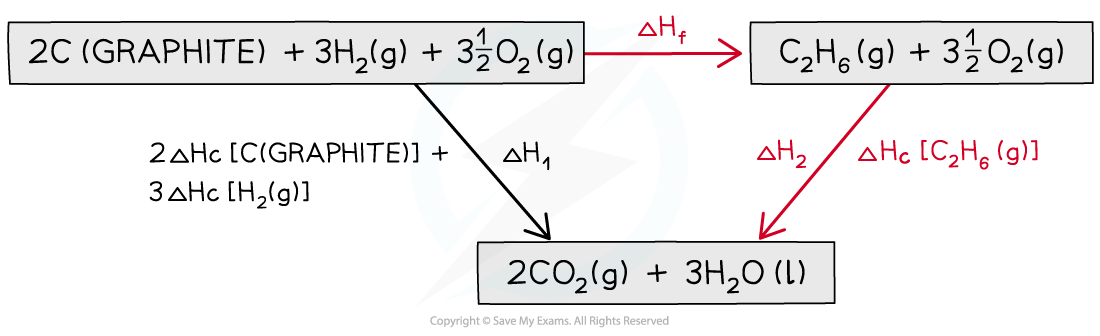
  • Step 4: Apply Hess’s Law:

    • ΔHf = ΔH1 – ΔH2

    • ΔHf = ( (2 x –393.5) + (3 x –285.8) ) – ( –1559.7)

    • ΔHf = –84.7 kJ mol-1 

Calculating average bond energies using Hess's cycles

  • Bond energies cannot be found directly so enthalpy cycles are used to find the average bond energy

  • This can be done using enthalpy changes of atomisation and combustion or formation

  • The enthalpy change of atomisation (ΔHθat ) is the enthalpy change when one mole of gaseous atoms is formed from its elements under standard conditions. (A Level only)

    • E.g. ΔHθat [H2] relates to the equation:

½H2 (g) → H (g)

Worked Example

Calculate the average bond energy of the C–H bond, using the relevant ΔHθf and ΔHθat values shown in the table.

 

Energy kJ mol-1 

ΔHθf  [CH4 (g)]

–74.8

ΔHθat [½H2 (g)]

+218

ΔHθat [C (graphite)]

+717.7

Answer

  • Step 1: Write down the equation for the dissociation of methane at the top

Bond energy cycle step 1: the dissociation of methane at the top, CH4(g) → C(g) + 4H(g).

  • Step 2: Write down the elements at the bottom

Bond energy cycle step 2: CH4(g) and C(g) + 4H(g) at the top, with the elements C(graphite) + 2H2(g) drawn below.

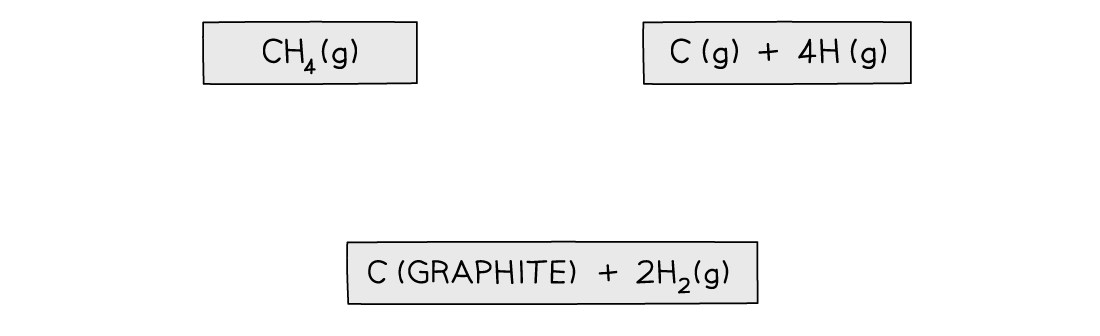
  • Step 3: Draw all arrows in the correct direction

Completed bond energy cycle: ΔH from CH4(g) to C(g) + 4H(g); ΔHf[CH4(g)] from the elements C(graphite) + 2H2(g) up to CH4(g); ΔHat[C(graphite)] + 4 x ΔHat[½H2(g)] from the elements up to C(g) + 4H(g).

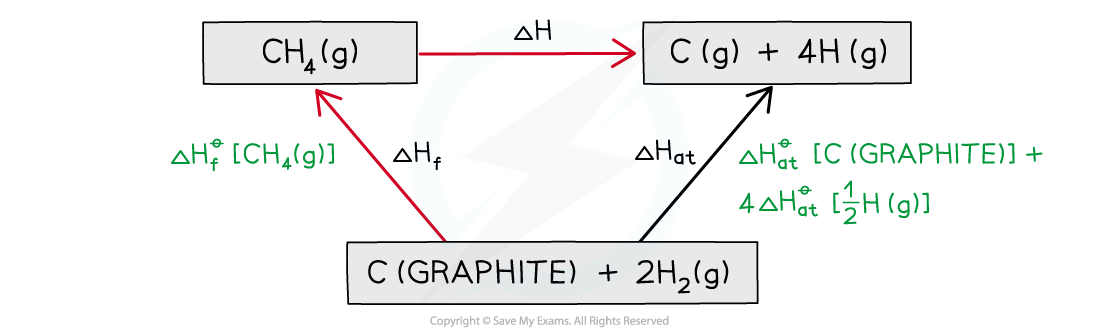
  • Step 4: Apply Hess’s Law:

    • ΔH = ΔHθat – ΔHf

    • ΔH = ( (+717.7) + (4 x 218) ) – ( –74.8)

    • ΔH = +1664.5 kJ mol-1 

  • Step 5: Calculate the bond energy for one C–H bond

    • There are 4 C-H bonds in methane

    • Average bond enthalpy (C–H) = +1664.54

    • Average bond energy (C–H) = +416 kJ mol-1 (to 3 significant figures)

Examiner Tips and Tricks

  • Remember to take into account the number of moles of each reactant and product.

  • For example, there are two moles of NaHCO3 (s) so the ΔHf value is multiplied by 2.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Our rating represented in Trustpilot stars
Read more reviews

Build on this topic

Check your understandingTry an Exam Question on this topicTest your recallReinforce key facts and definitions with Flashcards
Previous:Enthalpy & Bond EnergiesNext:Oxidation Number Rules
Caroline Carroll

Author: Caroline Carroll

Expertise: Head of Content Delivery

Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about delivering high-quality resources to help students achieve their full potential.