Calculations using Born-Haber Cycles (Cambridge (CIE) A Level Chemistry) : Revision Note
Calculations Using Born-Haber Cycles
Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlattꝋ) by applying Hess’s law and rearranging:
ΔHfθ = ΔHatθ + ΔHatθ + IE + EA + ΔHlattθ
If we simplify this into three terms, this makes the equation easier to see:
ΔHlattθ
ΔHfθ
ΔH1θ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
The simplified equation becomes
ΔHfθ = ΔH1θ + ΔHlattθ
So, if we rearrange to calculate the lattice energy, the equation becomes
ΔHlattθ = ΔHfθ - ΔH1θ
When calculating the ΔHlattθ, all other necessary values will be given in the question
A Born-Haber cycle could be used to calculate any stage in the cycle
For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
The principle would be exactly the same
Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl- ions
Worked Example
Using the data below, calculate the ΔHlattθ of potassium chloride, KCl.
| ΔHatθ / kJ mol–1 | IE / EA / kJ mol–1 |
|---|---|---|
K | +90 | +418 |
Cl | +122 | -349 |
ΔHfθ / kJ mol–1 | ||
KCl | -437 | |
Answer:
Step 1: The corresponding Born-Haber cycle is:
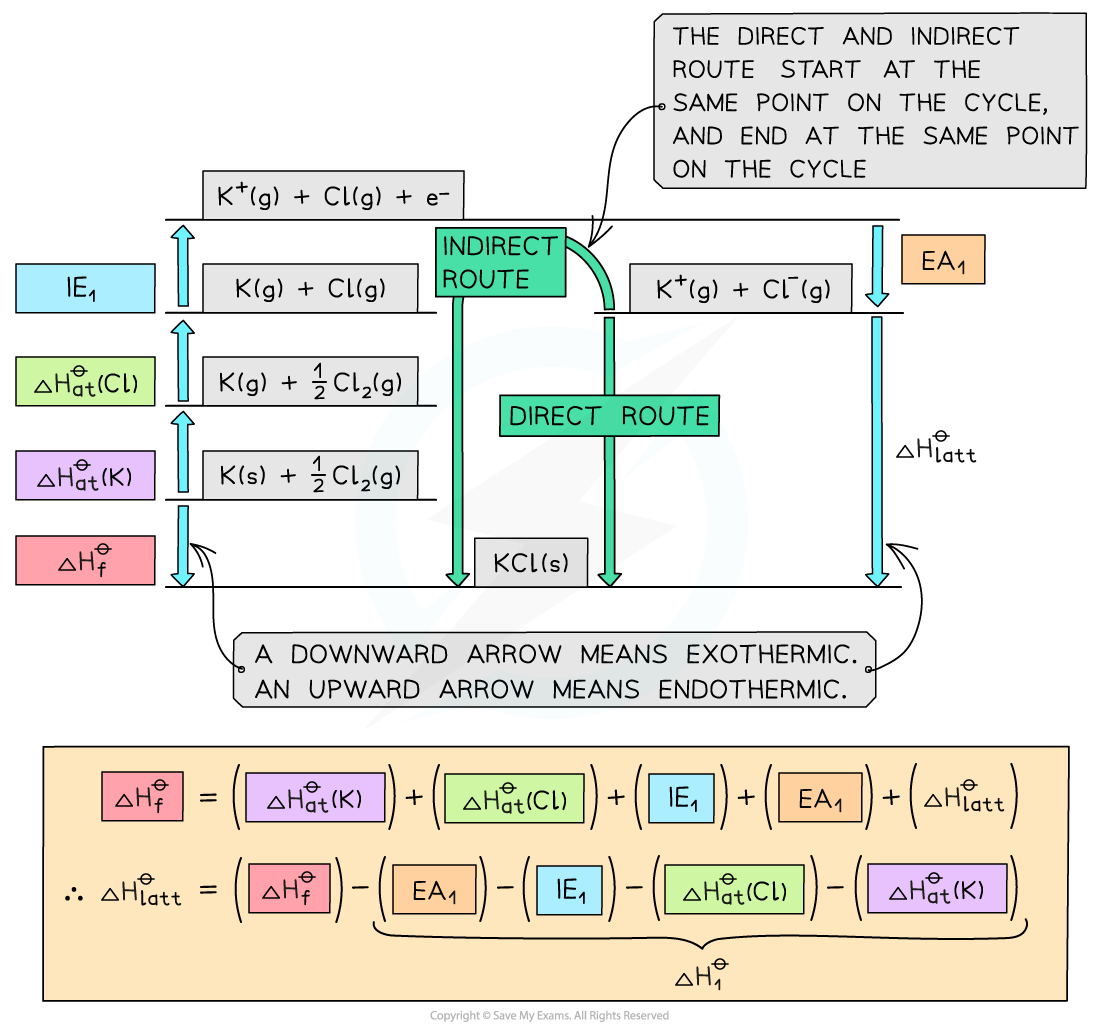
Step 2: Applying Hess’ law, the lattice energy of KCl is:
ΔHlattθ = ΔHfθ - ΔH1θ
ΔHlattθ = ΔHfθ - [(ΔHatθ K) + (ΔHatθ Cl) + (IE1 K) + (EA1 Cl)]
Step 3: Substitute in the numbers:
ΔHlattθ = (-437) - [(+90) + (+122) + (+418) + (-349)] = –718 kJ mol-1–1
Worked Example
Using the data below, calculate the ΔHlattθ of magnesium oxide, MgO.
| ΔHatθ / kJ mol–1 | IE1 / EA1 / kJ mol–1 | IE2 / EA2 / kJ mol–1 |
|---|---|---|---|
Mg | +148 | +736 | +1450 |
O | +248 | –142 | +770 |
ΔHfθ / kJ mol–1 | |||
MgO | –602 | ||
Answer:
Step 1: The corresponding Born-Haber cycle is:
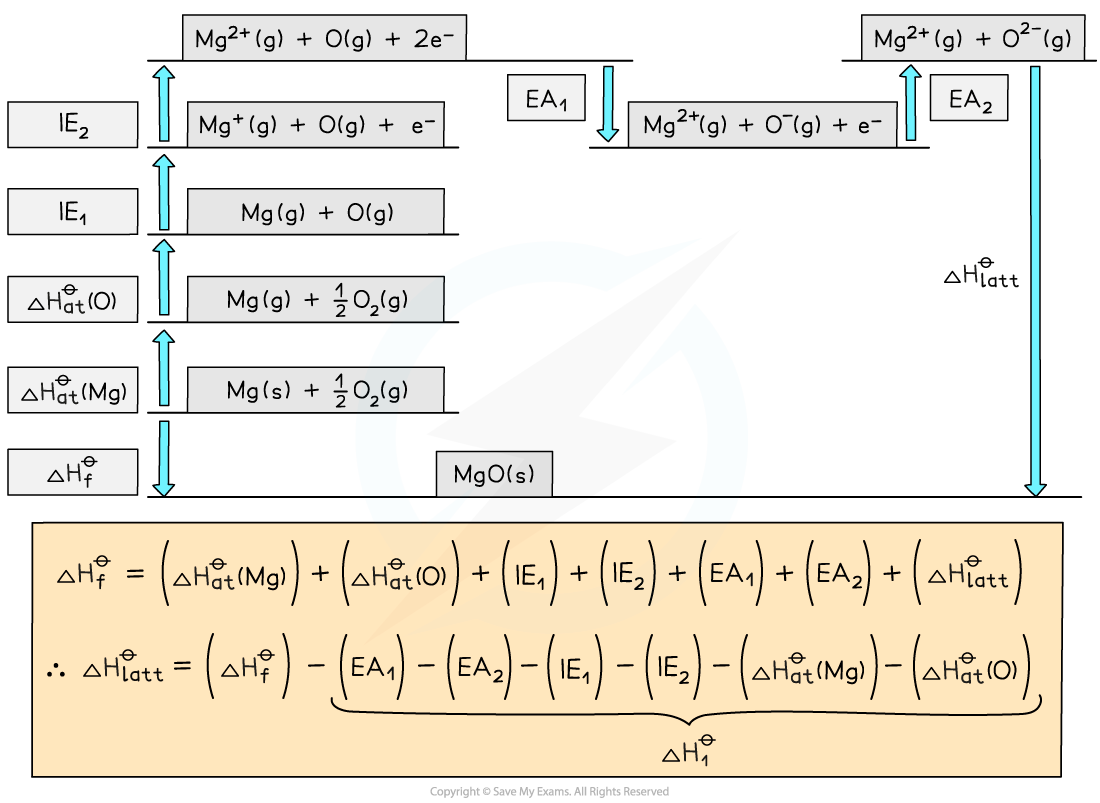
Step 2: Applying Hess’ law, the lattice energy of MgO is:
ΔHlattθ = ΔHfθ - ΔH1θ
ΔHlattθ = ΔHfθ - [(ΔHatθ Mg) + (ΔHatθ O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]
Step 3: Substitute in the numbers:
ΔHlattθ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
Examiner Tips and Tricks
Make sure you use brackets when carrying out calculations using Born-Haber cycles as you may forget a +/- sign which will affect your final answer!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
