Entropy of Vaporisation (AQA A Level Chemistry)

Entropy of Vaporisation

• The entropy change when water boils can be measured using a kettle and a top pan balance

• At the boiling point, liquid water and water vapour exist in equilibrium so the free energy change is 0

• Rearranging the Gibbs equation allows us to find the entropy change using the enthalpy change:

ΔG^ꝋ = ΔH^ꝋ – TΔS^ꝋ = 0 

ΔH^ꝋ = TΔS^ꝋ

ΔS^ꝋ = ΔH^ꝋ / T

• The sequence is:

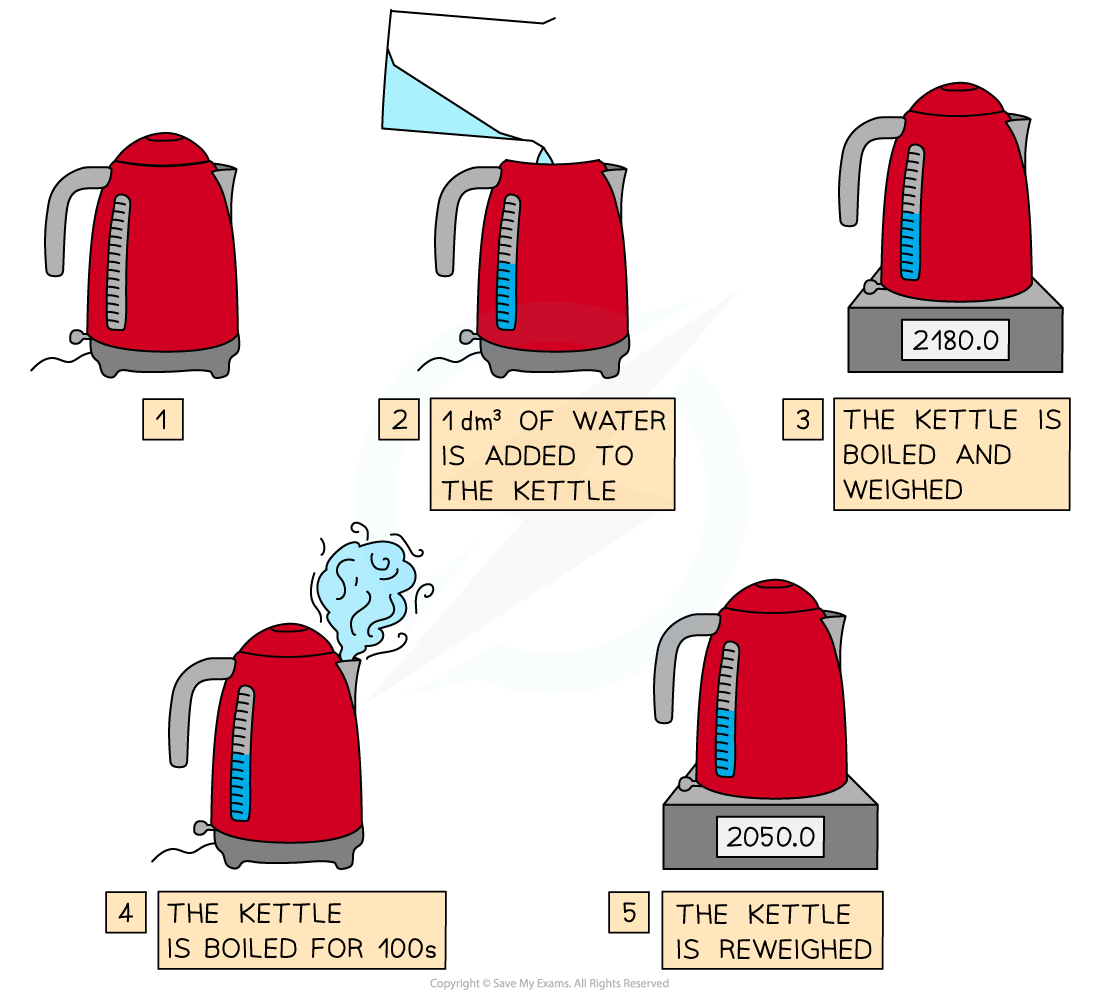
Determining the entropy of vaporisation by measuring the enthalpy change of boiling water

Steps in the procedure

• A fixed volume of water is measured and added to an electric kettle - a suitable amount to use is 1 dm³

• The power rating of the kettle must be known - it will usually be marked somewhere on the kettle

• The water is boiled and then the kettle is switched off and weighed

• The water is re-boiled by keeping the automatic cut-off switch depressed for 100 s

• The kettle and contents are then re-weighed to find out how much water has been lost by evaporation

Practical tips

• Make sure you have a balance that can read up to at least 2.5 kg

  • If you don't, you can weigh the water before and after the experiment in a lightweight container such as a plastic box or reduce the volume of water

• The actual amount of water you use does not really matter as long as you can measure it and it covers the heating element in the kettle

Specimen Results

• Here is a set of typical results for this experiment

Specimen Results Table

Analysis

• Household kettles have a typical power rating of 2 - 3 kW

• Suppose you use a 3 kW kettle for this experiment; this means the kettle supplies 3 kJ of energy per second

• If you boil the kettle for 100 s, then the kettle has supplied 300 kJ of energy to the water

• Using the specimen results we can see that 130 g of water have boiled away, so the number of moles of water that evaporated are:

moles of water evaporated = 130 / 18 = 7.22 mol

• The enthalpy change in kJ per mole of water is therefore:

enthalpy of vaporisation of water = 300 / 7.22 = 41.55 kJ mol^-1

• Changing this to J per mole gives:

enthalpy of vaporisation of water = 41.55 x 1000 = 41 550 J mol^-1

• The temperature in Kelvin at which water boils is:

temperature in Kelvin =  100 + 273 =  373 K

• Substituting into the equation gives a value for the entropy of vaporisation of water

ΔS^ꝋ = ΔH^ꝋ / T

ΔS^ꝋ = 41 550 / 373 = 111.4 J mol^-1