Reaction Feasibility (AQA A Level Chemistry)

• The Gibbs equation can be used to calculate whether a reaction is feasible or not

ΔG^ꝋ = ΔH_reaction^ꝋ - TΔS_system^ꝋ

• When ΔG^ꝋ is negative, the reaction is feasible and likely to occur
• When ΔG^ꝋis positive, the reaction is not feasible and unlikely to occur
• Feasible and spontaneous are fairly similar terms to describe reactions
  • Feasible tends to be used to describe reactions which are energetically favourable, so reactions that should go
  • Spontaneous tends to be used to describe reactions that go of their own accord
    

  Summary for temperature and Gibbs free energy 

  

Answer

Step 1: Calculate ΔS_system^ꝋ

ΔS_system^ꝋ = ΣΔS_products^ꝋ - ΣΔS_reactants^ꝋ

ΔS_system^ꝋ = (2 x ΔS^ꝋ [CaO(s)]) -  (2 x ΔS^ꝋ [Ca(s)] + ΔS^ꝋ [O₂(g)])

= (2 x 40.00) - (2 x 41.00 + 205.0)

= -207.0 J K^-1 mol^-1

Step 2: Convert ΔS^ꝋ to kJ K^-1 mol^-1

= -207.0 J K^-1 mol^-1÷ 1000 = -0.207 kJ mol^-1

Step 3: Calculate ΔG^ꝋ

ΔG^ꝋ = ΔH_reaction^ꝋ - TΔS_system^ꝋ

= -635.5 - (298 x -0.207)

= -573.8 kJ mol^-1

Step 4: Determine whether the reaction is feasible

Since the ΔG^ꝋ is negative the reaction is feasible

• The feasibility of a reaction can be affected by the temperature
• The Gibbs equation will be used to explain what will affect the feasibility of a reaction for exothermic and endothermic reactions

Exothermic reactions

• In exothermic reactions, ΔH_reaction^ꝋ is negative
• If the ΔS_system^ꝋ is positive:
  • Both the first and second term will be negative
  • Resulting in a negative ΔG^ꝋ so the reaction is feasible
  • Therefore, regardless of the temperature, an exothermic reaction with a positive ΔS_system^ꝋ will always be feasible

• If the ΔS_system^ꝋ is negative:
  • The first term is negative and the second term is positive
  • At very high temperatures, the -TΔS_system^ꝋ will be very large and positive and will overcome ΔH_reaction^ꝋ
  • Therefore, at high temperatures ΔG^ꝋ is positive and the reaction is not feasible

• Since the relative size of an entropy change is much smaller than an enthalpy change, it is unlikely that TΔS > ΔH as temperature increases
• These reactions are therefore usually spontaneous at normal conditions

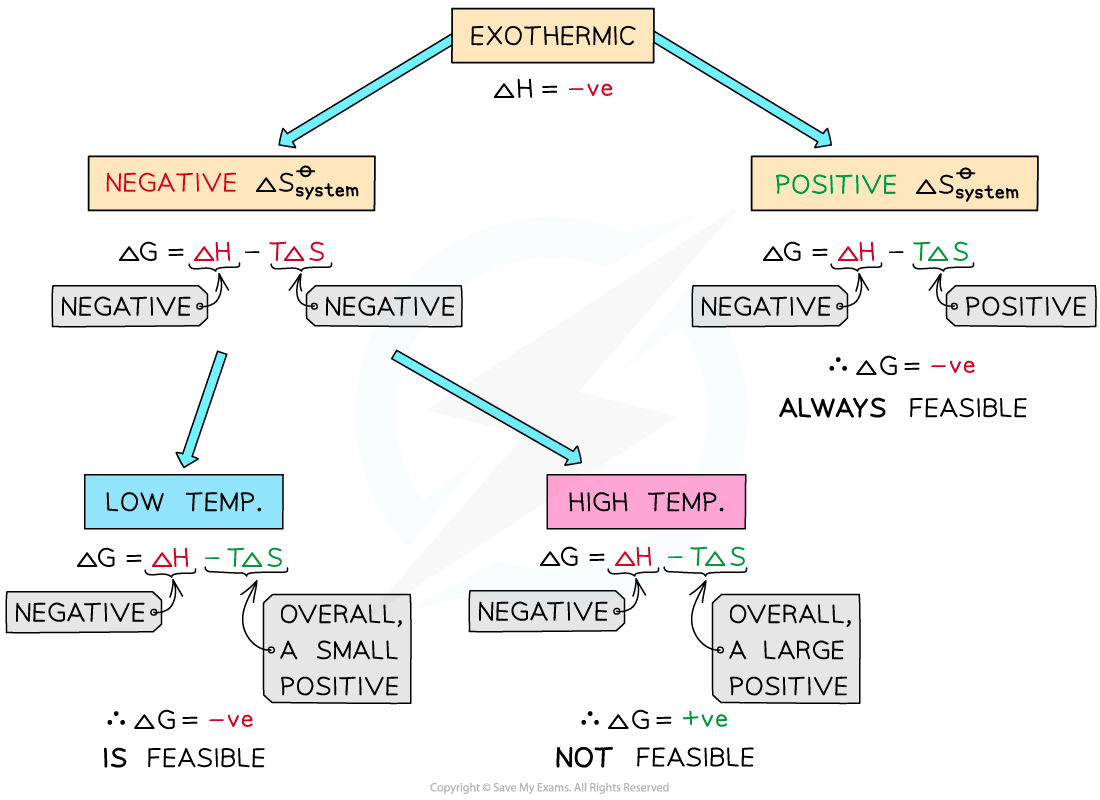
The diagram shows under which conditions exothermic reactions are feasible

Endothermic reactions

• In endothermic reactions, ΔH_reaction^ꝋ is positive
• If the ΔS_system^ꝋ is negative:
  • Both the first and second term will be positive
  • Resulting in a positive ΔG^ꝋ so the reaction is not feasible
  • Therefore, regardless of the temperature, endothermic with a negative ΔS_system^ꝋ will never be feasible

• If the ΔS_system^ꝋ is positive:
  • The first term is positive and the second term is negative
  • At low temperatures, the -TΔS_system^ꝋ will be small and negative and will not overcome the larger ΔH_reaction^ꝋ
  • Therefore, at low temperatures ΔG^ꝋ is positive and the reaction is not feasible
  • The reaction is more feasible at high temperatures as the second term will become negative enough to overcome the ΔH_reaction^ꝋ resulting in a negative ΔG^ꝋ

• This tells us that for certain reactions which are not feasible at room temperature, they can become feasible at higher temperatures
  • An example of this is found in metal extractions, such as the extraction if iron in the blast furnace, which will be unsuccessful at low temperatures but can occur at higher temperatures (~1500 ^oC in the case of iron)

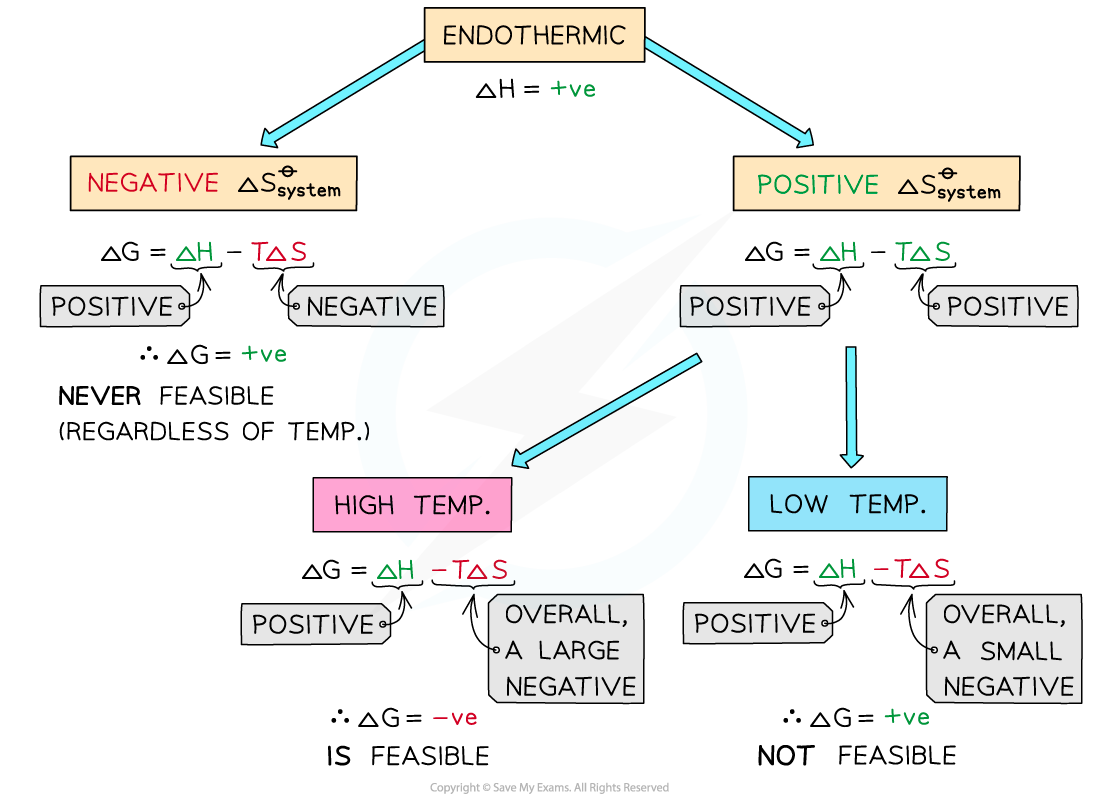
The diagram shows under which conditions endothermic reactions are feasible

A summary table of free energy conditions

• Rearranging the Gibbs equation allows you to determine the temperature at which a non-spontaneous reaction become feasible

ΔG^ꝋ = ΔH_reaction^ꝋ - TΔS_system^ꝋ

• For a reaction to be feasible ΔG^ꝋ must be zero or negative

0 = ΔH^ꝋ - TΔS^ꝋ

ΔH^ꝋ = TΔS^ꝋ

T = ΔH^ꝋ / ΔS^ꝋ

Answer:

If ΔG = 0 then ,   T = ΔH^ꝋ / ΔS^ꝋ

T = 1336 ÷ (581/1000)

T = 2299 K

Graphing the Gibbs Equation

• The Gibbs equation can be expressed as the equation for a straight line 

 ΔG^ꝋ = ΔH^ꝋ - TΔS^ꝋ 

ΔG^ꝋ = - ΔS^ꝋT  + ΔH^ꝋ 

y = mx + c

• A graph of free energy versus temperature (in K) will give a straight line, with slope -ΔS^ꝋ and y-intercept, ΔH^ꝋ.
• The variation of ΔG^ꝋ against T for the synthesis of ammonia has been plotted below:

N₂ (g) + 3H₂ (g)⇌ 2NH₃ (g)

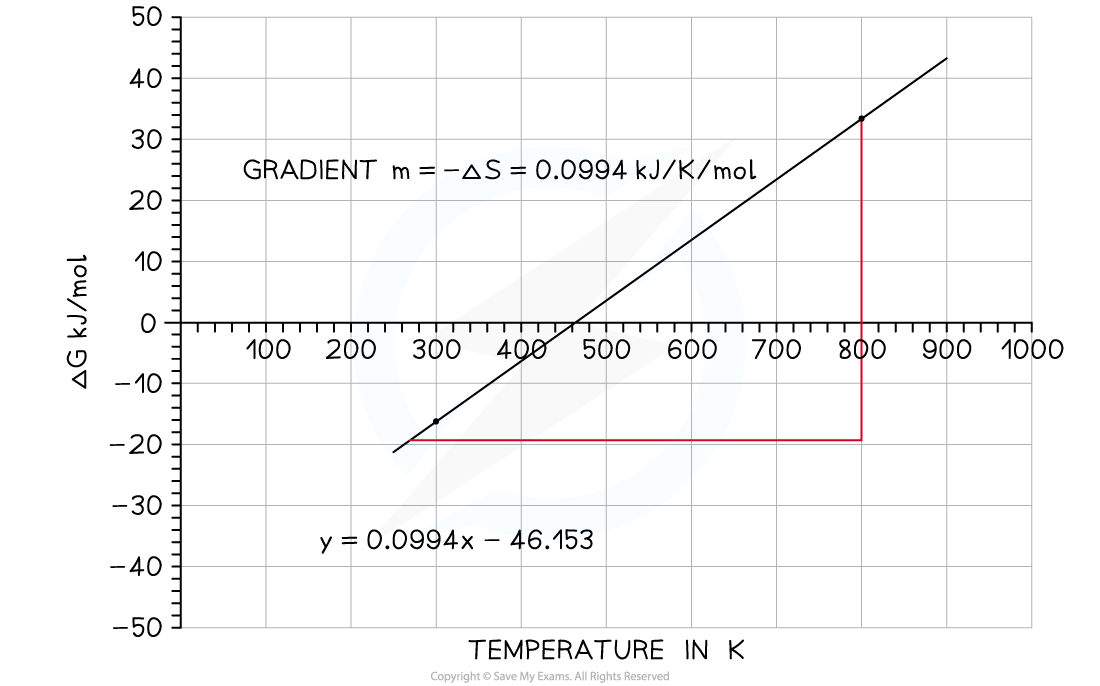
Graph of free energy versus temperature for the synthesis of ammonia

• From this graph you should be able to see some key features:
  • The x-intercept shows you where the reaction ceases to be spontaneous, in this case at 460 K (187 ^oC)
  • Above this temperature ΔG^ꝋ is positive so the reaction is not feasible
    • However, you may recall that the operating conditions of the Haber process are higher than this temperature, but this graph takes no account of the use of a catalyst which affects the energetics of the system, nor does it take into account anything about the rate of reaction or the fact that it is an equilibrium and removal of the ammonia as soon as it is formed also tips the balance in favour of the product

  • The y-intercept shows you reaction is exothermic which you can see from the enthalpy of formation; the value is approximately -46 kJ mol ^-1
  • An exothermic equilibrium reaction would be favoured by lower temperatures - this is seen by the value of ΔG^ꝋ  becoming increasingly negative as the temperature falls