The Ideal Gas Equation (AQA A Level Chemistry)
Revision Note
The Ideal Gas Equation
Kinetic theory of gases
The kinetic theory of gases states that molecules in gases are constantly moving
The theory makes the following assumptions:
That gas molecules are moving very fast and randomly
That molecules hardly have any volume
That gas molecules do not attract or repel each other (no intermolecular forces)
No kinetic energy is lost when the gas molecules collide with each other (elastic collisions)
The temperature of the gas is related to the average kinetic energy of the molecules
Gases that follow the kinetic theory of gases are called ideal gases
However, in reality gases do not fit this description exactly but may come very close and are called real gases
Ideal gases
The volume that an ideal gas occupies depends on:
Its pressure
Its temperature
When a gas is heated (at constant pressure) the particles gain more kinetic energy and undergo more frequent collisions with the container wall
To keep the pressure constant, the molecules must get further apart and therefore the volume increases
The volume is therefore directly proportional to the temperature (at constant pressure)
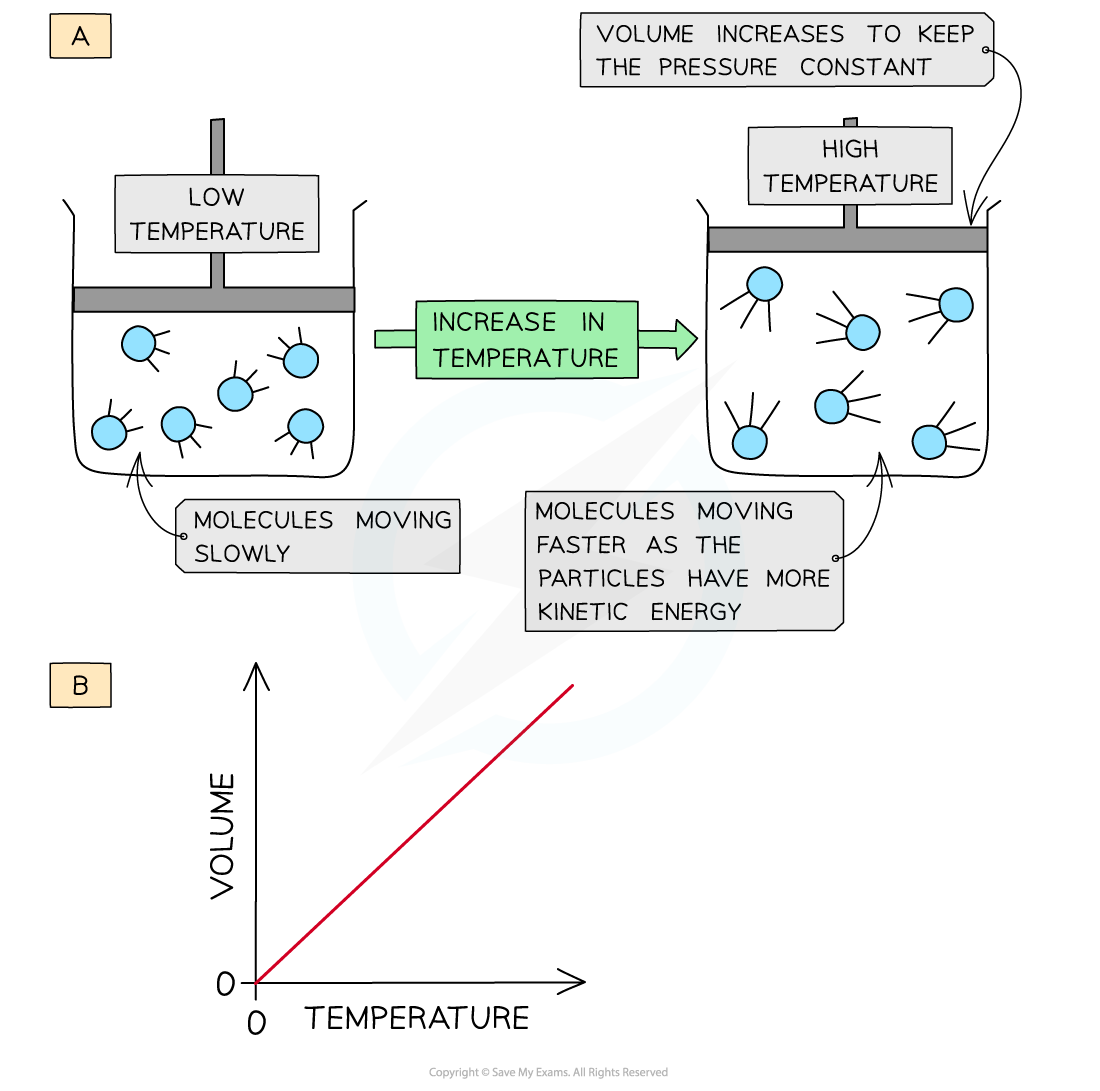
The volume of a gas increases upon heating to keep a constant pressure (a); volume is directly proportional to the temperature (b)
Limitations of the ideal gas law
At very low temperatures and high pressures real gases do not obey the kinetic theory as under these conditions:
Molecules are close to each other
There are instantaneous dipole- induced dipole or permanent dipole- permanent dipole forces between the molecules
These attractive forces pull the molecules away from the container wall
The volume of the molecules is not negligible
Real gases therefore do not obey the following kinetic theory assumptions at low temperatures and high pressures:
There is zero attraction between molecules (due to attractive forces, the pressure is lower than expected for an ideal gas)
The volume of the gas molecules can be ignored (volume of the gas is smaller than expected for an ideal gas)
Ideal gas equation
The ideal gas equation shows the relationship between pressure, volume, temperature and number of moles of gas of an ideal gas:
PV = nRT
P = pressure (pascals, Pa)
V = volume (m3)
n = number of moles of gas (mol)
R = gas constant (8.31 J K-1 mol-1)
T = temperature (kelvin, K)
Worked Example
Calculating the volume of a gas
Calculate the volume occupied by 0.781 mol of oxygen at a pressure of 220 kPa and a temperature of 21 °C.
Answer
Rearrange the ideal gas equation to find volume of gas
V =
Check and convert values to the correct units
P = 220 kPa = 220 000 Pa
n = 0.781 mol
R = 8.31 J K-1 mol-1
T = 21 oC = 294 K
Calculate the volume the oxygen gas occupies
V
Worked Example
Calculating the molar mass of a gas
A flask of volume 1000 cm3 contains 6.39 g of a gas. The pressure in the flask was 300 kPa and the temperature was 23 °C.
Calculate the relative molecular mass of the gas.
Answer:
Rearrange the ideal gas equation to find the number of moles of gas:
n =
Check and convert values to the correct units:
P = 300 kPa = 300 000 Pa
V = 1000 cm3 = 1 dm3 = 0.001 m3
R = 8.31 J K-1 mol-1
T = 23 oC = 296 K
Calculate the number of moles:
n =
= 0.12 mol
Calculate the molar mass using the number of moles of gas:
n =
molar mass =
= 53.25 g mol-1
Examiner Tips and Tricks
To calculate the temperature in Kelvin, add 273 to the Celsius temperature - e.g. 100 oC is 373 Kelvin.
You must be able to rearrange the ideal gas equation to work out all parts of it.
The units are incredibly important in this equation - make sure you know what units you should use, and do the necessary conversions when doing your calculations!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
