Variation: t-test Method (CIE A Level Biology)

• A statistical test called the t-test can be used to compare the means of two sets of data and determine whether they are significantly different or not
  • The formula for the t-test will be provided in the exam, but formulae for how to calculate the number of degrees of freedom is not provided in the exam and must be learnt

• The sets of data must follow a roughly normal distribution, and be continuous and the standard deviations should be approximately equal
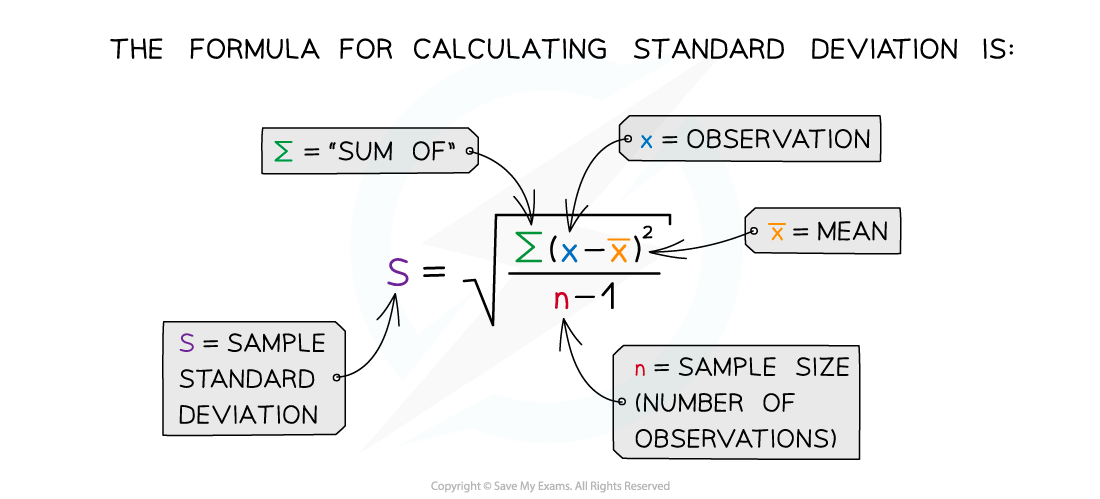
• The standard deviation (s) must be calculated for each data set before the t-test can be carried out
• A null hypothesis should also be given
  • This is a statement of what we would expect if there is no significant difference between two means, and that any differences seen are due to chance

• If there is a statistically significant difference between the means of two sets of data, then the observation is not down to chance and the null hypothesis can be rejected

Calculating the standard deviation

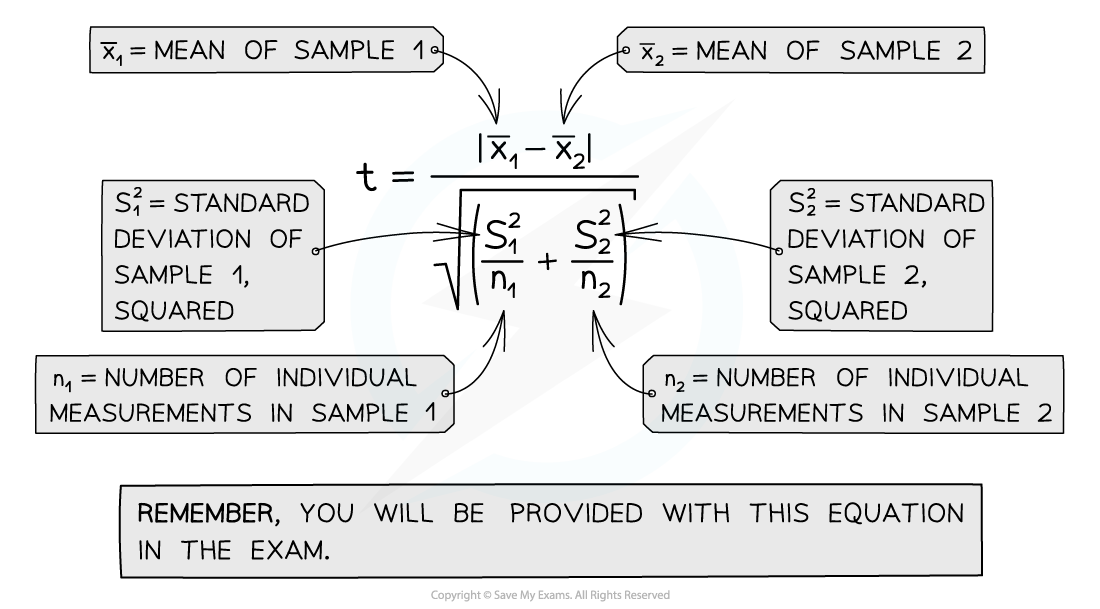
Using the t-test to compare two means

• The steps below outline the general steps in a t-test; for a worked example, see the next page
• Null hypothesis: there is no statistically significant difference between the means of sample 1 and sample 2
• Step 1:  Calculate the mean for each data set:

x̄₁ is the mean for sample 1, and x̄₂ is the mean for sample 2

• Step 2:  Calculate the standard deviation for each set of data, s₁ = standard deviation of sample 1 and s₂ = standard deviation of sample 2

• Step 3:  Square the standard deviation and divide by n (the number of observations) in each sample, for both samples:

• Step 4:  Add the values from step 3 together and take the square root:

• Step 5:  Divide the difference between the two means (see step 1) with the value calculated in step 4 to get the t value:

• Step 6:  Calculate the degrees of freedom (v) for the whole data set (remember the formulae for this will not be given in the exam):

   

• Step 7:  Look at a table that relates t values to the probability that the differences between data sets is due to chance to find where the t value for the degrees of freedom (v) calculated lies

T values table

• Step 8:  The greater the t value calculated (for any degree of freedom), the lower the probability of chance causing any significant difference between the two sample means
  • Identify where the t value calculated lies with respect to the confidence levels provided
  • If the t value is greater than the critical value (obtained from the table at a probability level of 0.05) then any difference between the means of the two data sets is said to be statistically significant
    • There is a less than 5 % probability that any difference is due to chance
    • The null hypothesis can be rejected
  • If the t value is less than the critical value (obtained from the table at a probability level of 0.05) then there is no significant difference between the means of the two data sets
    • The probability that any difference is due to chance is higher than 5 %
    • The null hypothesis is accepted
• Using the table above, if a value of t was calculated to be 2.38 at 5 degrees of freedom, then it lies between the critical values of 2.02 and 2.57
• Therefore, the probability that chance produced any difference between the two means is between 5 and 10 %; this is a higher than 5 % probability that the difference is due to chance
• The null hypothesis would be accepted and it would be said that there is no significant difference between the data sets