Maths Skill: Using Logarithms When Investigating Bacteria (AQA A Level Biology)

Maths Skill: Using Logarithms When Investigating Bacteria

• Bacterial colonies can grow at rapid rates when in culture with very large numbers of bacteria produced within hours

• Dealing with the experimental data relating to large numbers of bacteria can be difficult when using traditional linear scales

  • There is a wide range of very small and very large numbers

  • This makes it hard to work out a suitable scale for the axes of graphs

• Logarithmic scales can be very useful when investigating bacteria

Using logarithms to deal with orders of magnitude

• Logarithmic scales allow for a wide range of values to be displayed on a single graph

• For example, yeast cells were grown in culture over several hours. The number of cells increased very rapidly from the original number of cells present

• The results from the experiment are shown in the graph below, using a log scale

  • The number of yeast cells present at each time interval was converted to a logarithm before being plotted on the graph

  • The log scale is easily identifiable as there are not equal intervals between the numbers on the y-axis

  • The wide range of cell numbers fit easily onto the same scale

Image showing the number of yeast cells grown in culture over 10 hours, using a logarithmic scale

• The pH scale is logarithmic

  • The concentration of hydrogen ions varies massively between each pH level

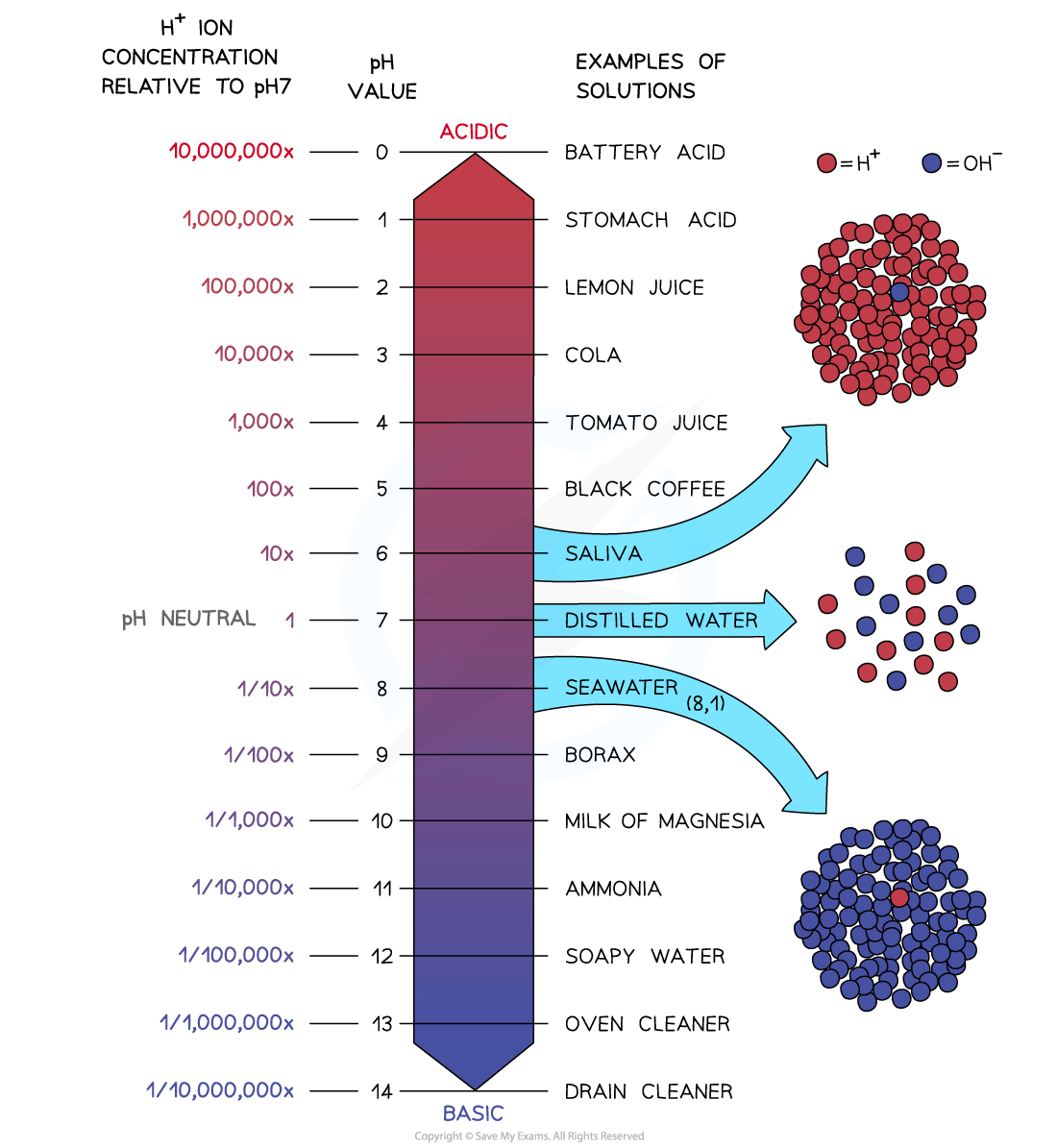
Image showing the range of hydrogen ion concentrations within the pH scale