Maths Skill: Using a Tangent to Find Initial Rate of Reaction (AQA A Level Biology)
Revision Note
Written by: Lára Marie McIvor
Reviewed by: Lucy Kirkham
Maths Skill: Using a Tangent to Find Initial Rate of Reaction
For linear graphs (i.e. graphs with a straight-line), the gradient is the same throughout
This makes it easy to calculate the rate of change (rate of change = change ÷ time)
However, many enzyme rate experiments produce non-linear graphs (i.e. graphs with a curved line), meaning they have an ever-changing gradient
They are shaped this way because the reaction rate is changing over time
In these cases, a tangent can be used to find the reaction rate at any one point on the graph:
A tangent is a straight line that is drawn so it just touches the curve at a single point
The slope of this tangent matches the slope of the curve at just that point
You then simply find the gradient of the straight line (tangent) you have drawn
The initial rate of reaction is the rate of reaction at the start of the reaction (i.e. where time = 0)
Worked Example
The graph below shows the results of an enzyme rate reaction. Using this graph, calculate the initial rate of reaction.
Step 1: Estimate the extrapolated curve of the graph
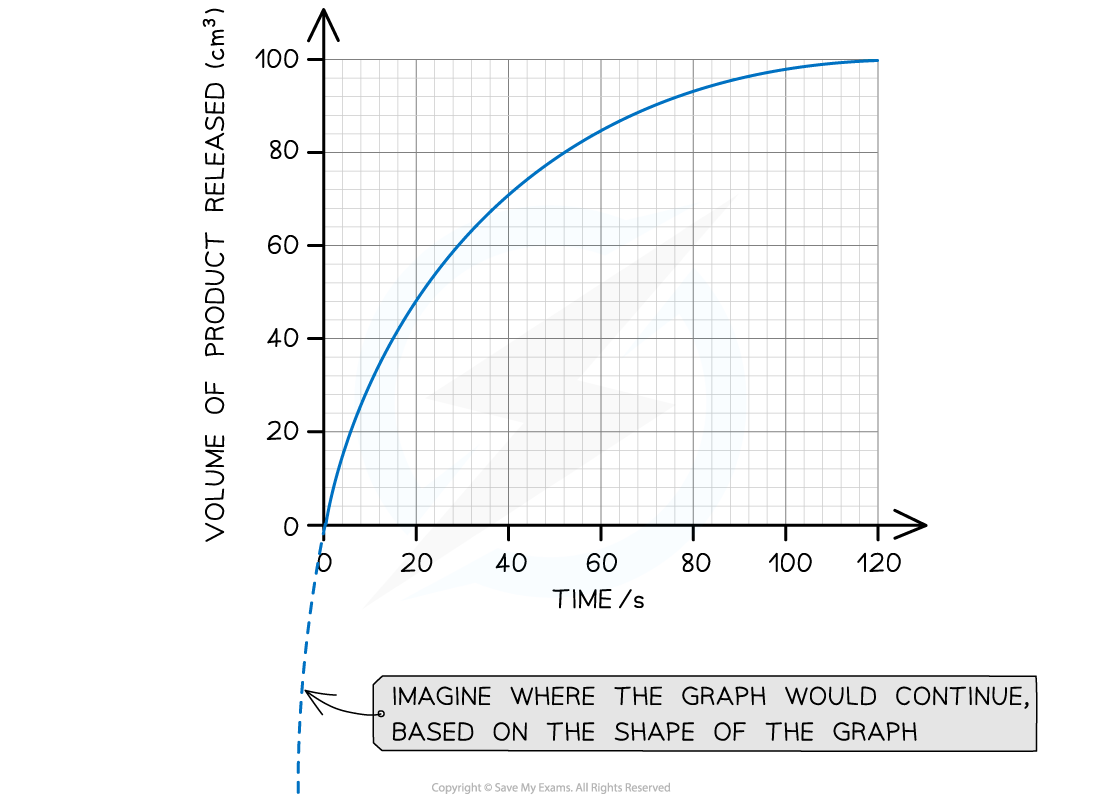
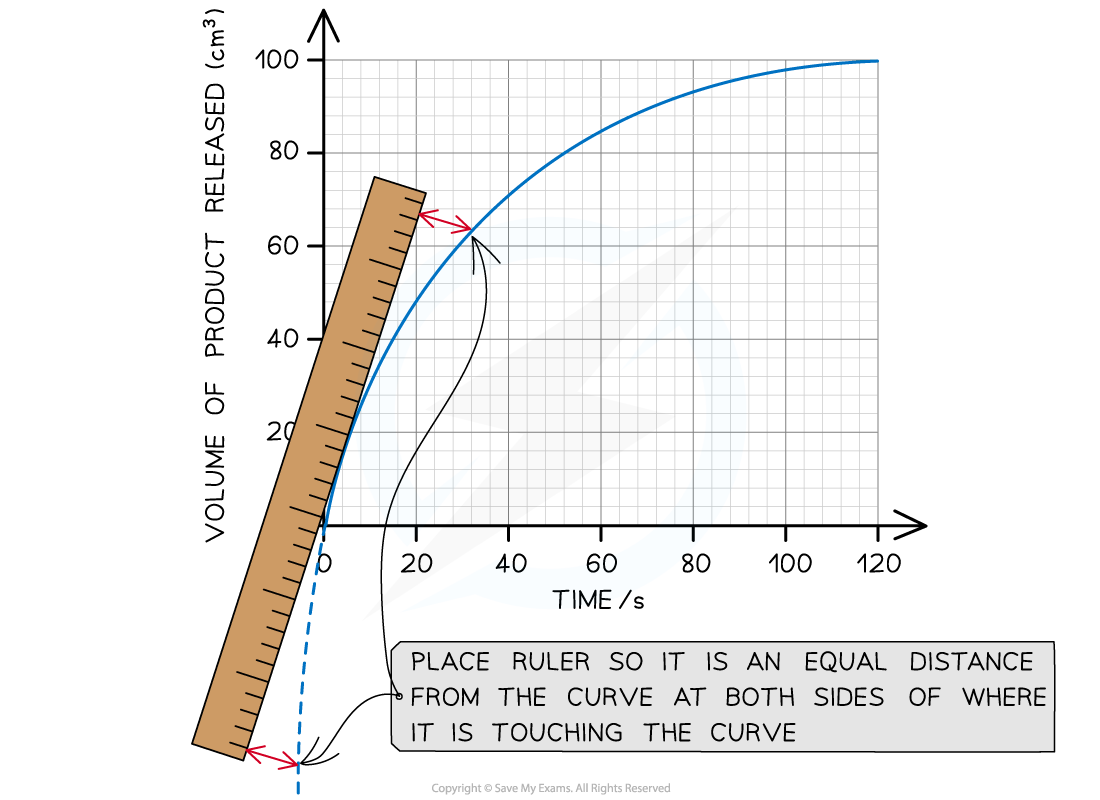
Step 2: Find the tangent to the curve at 0 seconds (the start of the reaction)
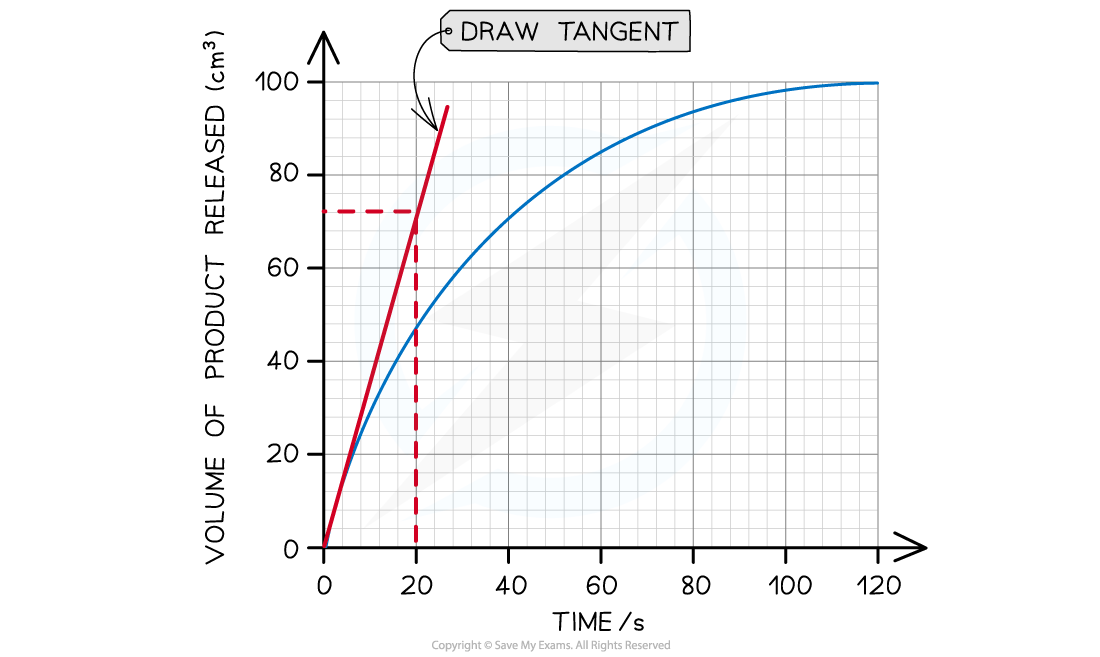
The tangent drawn in the graph above shows that 72 cm3 of product was produced in the first 20 seconds.Step 3: Calculate the gradient of the tangent (this will give you the initial rate of reaction):
Gradient = change in y-axis ÷ change in x-axis
Initial rate of reaction = 72 cm3 ÷ 20 s
Initial rate of reaction = 3.6 cm3 s-1
Examiner Tips and Tricks
When drawing tangents: always use a ruler and a pencil; make sure the line you draw is perfectly straight; choose the point where the tangent is to be taken and slowly line the ruler up to that point; try to place your ruler so that none of the line of the curve is covered by the ruler (it is much easier if the curve is entirely visible whilst the tangent is drawn).There is a handy phrase to help you remember how to calculate the gradient of a tangent or line. Rise over run means that any increase/decrease vertically should be divided by any increase/decrease horizontally.
Last updated:
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
