Types of Graphs (Edexcel IGCSE Maths)

Revision Note

Test yourself Flashcards

Author

Daniel I

Last updated

17 March 2023

Did this video help you?

Types of Graphs

Why do we need to know what graphs look like?

Graphs are used in various aspects of mathematics – but in the real world they can take on specific meanings
For example a linear (straight line) graph could be the path a ship needs to sail along to get from one port to another
A quadratic graph can be used to map the trajectory of a football being kicked through the air

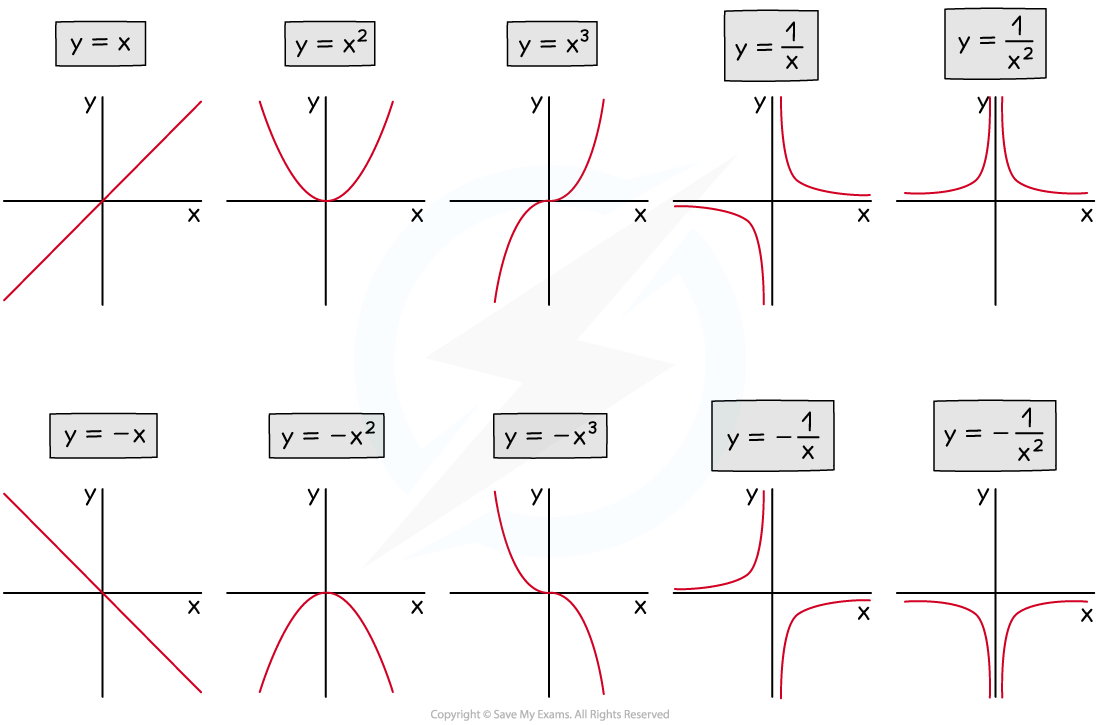
What are the shapes of graphs that we need to know?

Recalling facts alone won’t do much for boosting your GCSE Mathematics grade!
But being familiar with the general shapes of graphs will help you quickly recognise the sort of maths you are dealing with and features of the graph a question may refer to
Below the basic form of the five types of function (other than trig graphs) you need to recognise;
- linear ( $y = \pm x$ )
- quadratic ( $y = \pm x^{2}$ )
- cubic ( $y = \pm x^{3}$ )
- reciprocal ( $y = \pm \frac{1}{x}$ )
- reciprocal squared( $y = \pm \frac{1}{x^{2}}$ )
In addition, you need to recognise the three basic trigonometric graphs- but these are dealt with in the next section.

xlwetfR4_edexcel-igcse-3-graphs-types-of-graphs-v2

Worked example

Match the graphs to the equations.

Graphs:

Equations:

(1) $y = 0.6 x + 2$ , (2) $y = - 0.7 x^{3}$ , (3) $y = \frac{4}{x}$ , (4) $y = - x^{2} + 3 x + 2$

Starting with the equations,
(1) is a linear equation (y = mx + c) so matches the only straight line, graph (C)
(2) is a cubic equation with a negative coefficient so matches graph (D)
(3) is a reciprocal equation (notice that it takes the same form as inverse proportion) with a positive coefficient so matches graph (A)
(4) is a quadratic equation with a negative coefficient so matches graph (B)

Graph (A) → Equation (3)

Graph (B) → Equation (4)

Graph (C) → Equation (1)

Graph (D) → Equation (2)

Did this video help you?

Drawing Graphs Using a Table

How do we draw a graph using a calculator to get the table of values?

Before you start, think what the graph might look like – see the previous notes on being familiar with shapes of graphs
Find the TABLE function on your CALCULATOR
Enter the FUNCTION – f(x)
(use ALPHA button and x or X, depending on make/model)
(Press = when finished)
(If you are asked for another function, g(x), just press enter again)
Enter Start, End and Step (gap between x values)
Press = and scroll up and down to see y values
PLOT POINTS and join with a SMOOTH CURVE
To avoid errors always put negative numbers in brackets and use the (-) key rather than the subtraction key
If your calculator does not have a TABLE function, then you will have to work out each y value separately using the normal mode on your calculator

Examiner Tip

When using the TABLE function of your calculator, double-check that your calculator's y-values are the same as any that are given in the question

Worked example

(a)

Complete the table of values for the function

y = x^{3} - 5 x + 2

$x$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$
$y$		$4$					$14$

Use the TABLE function on your calculator for

f (x) = x^{2} - x - 6

, starting at -3, ending at 3 and with steps of 1

If your calculator does not have a TABLE function then substitute the values of $x$ into the function one by one for the missing values, being careful to put negative numbers in brackets, e.g.

x = - 3, y = {(- 3)}^{3} - 5 (- 3) + 2 = - 10

$x$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$
$y$	$- 10$	$4$	$6$	$2$	$- 2$	$0$	$14$

(b)

On the grid provided, draw the graph of

y = x^{3} - 5 x + 2

for values of

x

from

- 3

3

Carefully plot the points from your table of values in (a) on the grid, noting the different scales on the and axes
For example, the first column represents the point $(- 3, - 10)$

After plotting the points, join them with a smooth curve- do not use a ruler!

2-14-drawing-graphs

It is best practice to label the curve with its equation

Quadratic Graphs

A quadratic is a function of the form $y = a x^{2} + b x + c$ where $a$ is not zero
They are a very common type of function in mathematics, so it is important to know their key features

What does a quadratic graph look like?

The shape made by a quadratic graph is known as a parabola
The parabola shape of a quadratic graph can either look like a “u-shape” or an “n-shape”
- A quadratic with a positive coefficient of $x^{2}$ will be a u-shape
- A quadratic with a negative coefficient of $x^{2}$ will be an n-shape
A quadratic will always cross the $y$ -axis
A quadratic may cross the $x$ -axis twice, once, or not at all
- The points where the graph crosses the $x$ -axis are called the roots
If the quadratic is a u-shape, it has a minimum point (the bottom of the u)
If the quadratic is an n-shape, it has a maximum point (the top of the n)
Minimum and maximum points are both examples of turning points

Quadratic Graphs Notes Diagram 1

How do I sketch a quadratic graph?

We could create a table of values for the function and then plot it accurately, however we often only require a sketch to be drawn, showing just the key features
The most important features of a quadratic are

Its overall shape; a u-shape or an n-shape
Its $y$ -intercept
Its $x$ -intercept(s), these are also known as the roots
Its minimum or maximum point (turning point)

If it is a positive quadratic ( $a$ in $a x^{2} + b x + c$ is positive) it will be a u-shape
If it is a negative quadratic ( $a$ in $a x^{2} + b x + c$ is negative) it will be an n-shape
The $y$ -intercept of $y = a x^{2} + b x + c$ will be $(0, c)$
The roots, or the $x$ -intercepts will be the solutions to $y = 0$ ; $a x^{2} + b x + c = 0$

You can solve a quadratic by factorising, completing the square, or using the quadratic formula
There may be 2, 1, or 0 solutions and therefore 2, 1, or 0 roots

The minimum or maximum point of a quadratic can be found by;

Completing the square

Once the quadratic has been written in the form $y = p {(x - q)}^{2} + r$ , the minimum or maximum point is given by $(q, r)$
Be careful with the sign of the x-coordinate. E.g. if the equation is $y = {(x - 3)}^{2} + 2$ then the minimum point is $(3, 2)$ but if the equation is $y = {(x + 3)}^{2} + 2$ then the minimum point is $(- 3, 2)$

Using differentiation

Solving $\frac{d y}{d x} = 0$ will find the $x$ -coordinate of the minimum or maximum point
You can then substitute this into the equation of the quadratic to find the $y$ -coordinate

Worked example

Sketch the graph of $y = x^{2} - 5 x + 6$ showing the $x$ and $y$ intercepts

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at (0,6)

Factorise

$y = (x - 2) (x - 3)$

Solve $y = 0$

$(x - 2) (x - 3) = 0$

$x = 2 or x = 3$

So the roots of the graph are

(2,0) and (3,0)

cie-igcse-quadratic-graphs-we-1

Sketch the graph of $y = x^{2} - 6 x + 13$ showing the $y$ -intercept and the turning point

It is a positive quadratic, so will be a u-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the y-axis at

(0,13)

We can find the minimum point (it will be a minimum as it is a positive quadratic) by completing the square:

$x^{2} - 6 x + 13 = {(x - 3)}^{2} - 9 + 13 = {(x - 3)}^{2} + 4$

This shows that the minimum point will be

(3,4)

As the minimum point is above the $x$ -axis, this means the graph will not cross the $x$ -axis i.e. it has no roots

We could also show that there are no roots by trying to solve $x^{2} - 6 x + 13 = 0$

If we use the quadratic formula, we will find that $x$ is the square root of a negative number, which is not a real number, which means there are no real solutions, and hence no roots

cie-igcse-quadratic-graphs-we-2

Sketch the graph of $y = - x^{2} - 4 x - 4$ showing the root(s), $y$ -intercept, and turning point

It is a negative quadratic, so will be an n-shape

The $+ c$ at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at (0, -4)

We can find the maximum point (it will be a maximum as it is a negative quadratic) by completing the square:

$- x^{2} - 4 x - 4 = - 1 (x^{2} + 4 x + 4) = - 1 ({(x + 2)}^{2} - 4 + 4) = - {(x + 2)}^{2}$

This shows that the maximum point will be

(-2, 0)

As the maximum is on the $x$ -axis, there is only one root

We could also show that there is only one root by solving $- x^{2} - 4 x - 4 = 0$

If you use the quadratic formula, you will find that the two solutions for $x$ are the same number; in this case -2

cie-igcse-quadratic-graphs-we-3

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Flashcards

Did this page help you?

Previous:Parallel & Perpendicular LinesNext:Graphical Solutions

Types of Graphs (Edexcel IGCSE Maths)

Revision Note

Why do we need to know what graphs look like?

What are the shapes of graphs that we need to know?

How do we draw a graph using a calculator to get the table of values?

What does a quadratic graph look like?

How do I sketch a quadratic graph?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Daniel I